Beräkna Klippans höjd
Hej,
Man ska använda sinusatsen eller cosinussatsen.
Fråga 4369.

Jag vet att följande är fel men det är så jag gjort nu :p
Jag tänkte att 31° - 22° ger 9°.
Dividerar man 12 med 9 får man att varje grad ger ~1.33 mm
Det är kvar 22grader till havsytan, så 22*1.33 = 29,33 meter.
Fick ett till svar nu, 28.74 med sinusatsen. Men det är bara en chansning och kändes inte logiskt.
Man brukar ju vilja ha 3 parametrar med sig.. vilket man inte har.. så tänkte om det gick att använda likformighet på något sätt
Nu tänkte jag såhär..
Men det utgår ifrån att det är en 90° vinkel i triangeln vilket man egentligen inte vet ifrån bilden.
Det räknar också med att höjden 12 egentligen ska vara ritad ifrån centrum på masten istället för hypotenusan och att uppgiften är kryptisk med flit.. :p

Pröva att låta y beteckna det vågräta avståndet från observatören till en punkt rakt under masten.
Låt x vara klippans höjd.
Då har du två rätvinkliga trianglar med kända vinklar.
Pröva sedan något med tangensfunktionen.
Jag kan inte mer. Då får jag två trianglar som inte är likformiga varav den ena bara har två vinklar och ingen längd
Jo, såhär. Den lilla triangeln är likformig med hela triangeln.
Får ut längd 19.97 på den lilla triangelns andra katet. Men.. än sen då.
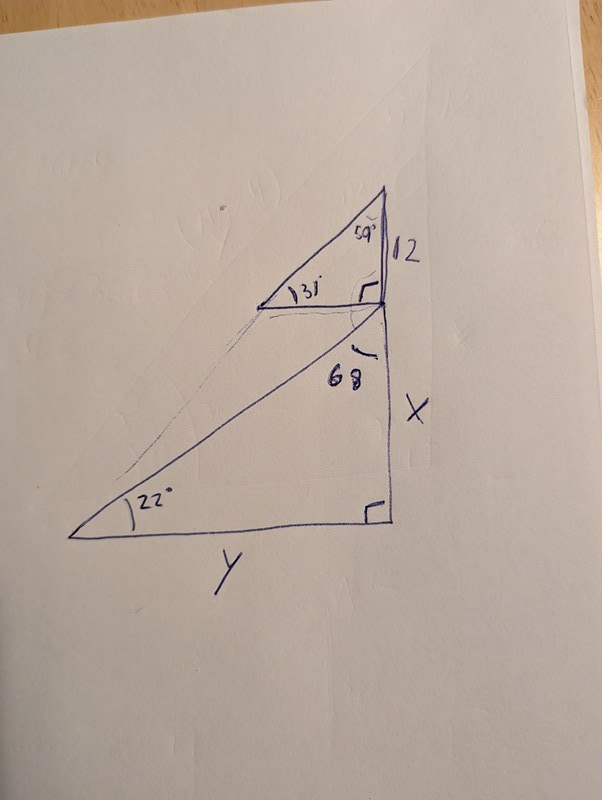
Den nedre triangeln är rätt. Den andra triangeln ska ha hypotenusan så som du suddat bort, en katet x+12 och en katet längs vattnet.
Ja precis
Tack! Jag hade inte kommit fram till det där själv.
Det visar sig att min post i #2 också är korrekt med sinusatsen.
Eller är det något felaktigt med den metoden i det här fallet? Kan ju råka komma fram till rätt svar av fel anledningar typ.
Facit använder också tangensmetoden.
Din metod i #2 är rätt.
Tack Ture.
Ha en bra dag






