Beräkna integral (med komplexa rötter)
Hej,
Jag har fastnat på följande uppgift:

Det som sker är att jag får tre rötter, varav två av dessa är komplexa.
Vanligtvis hade jag löst en sådan här uppgift med partialbråksuppdelning, men jag har aldrig stött på det med komplexa rötter. Gjorde ett försök och läste lite på internet, men utan framgång. Vilken strategi hade ni använt för att lösa denna uppgift?
Komplexa rötter brukar inte räknas när det gäller partialbråksuppdelning med reella tal/uttryck. Det går alltså utmärkt att se faktorerna x och x2-2x+2 som de två faktorerna i nämnaren, och partialbråksuppdela utifrån dem. :)
Smutstvätt skrev:Komplexa rötter brukar inte räknas när det gäller partialbråksuppdelning med reella tal/uttryck. Det går alltså utmärkt att se faktorerna x och x2-2x+2 som de två faktorerna i nämnaren, och partialbråksuppdela utifrån dem. :)
Tack snälla! Ska testa och se om jag kan lösa den nu :)
Smutstvätt skrev:Komplexa rötter brukar inte räknas när det gäller partialbråksuppdelning med reella tal/uttryck. Det går alltså utmärkt att se faktorerna x och x2-2x+2 som de två faktorerna i nämnaren, och partialbråksuppdela utifrån dem. :)
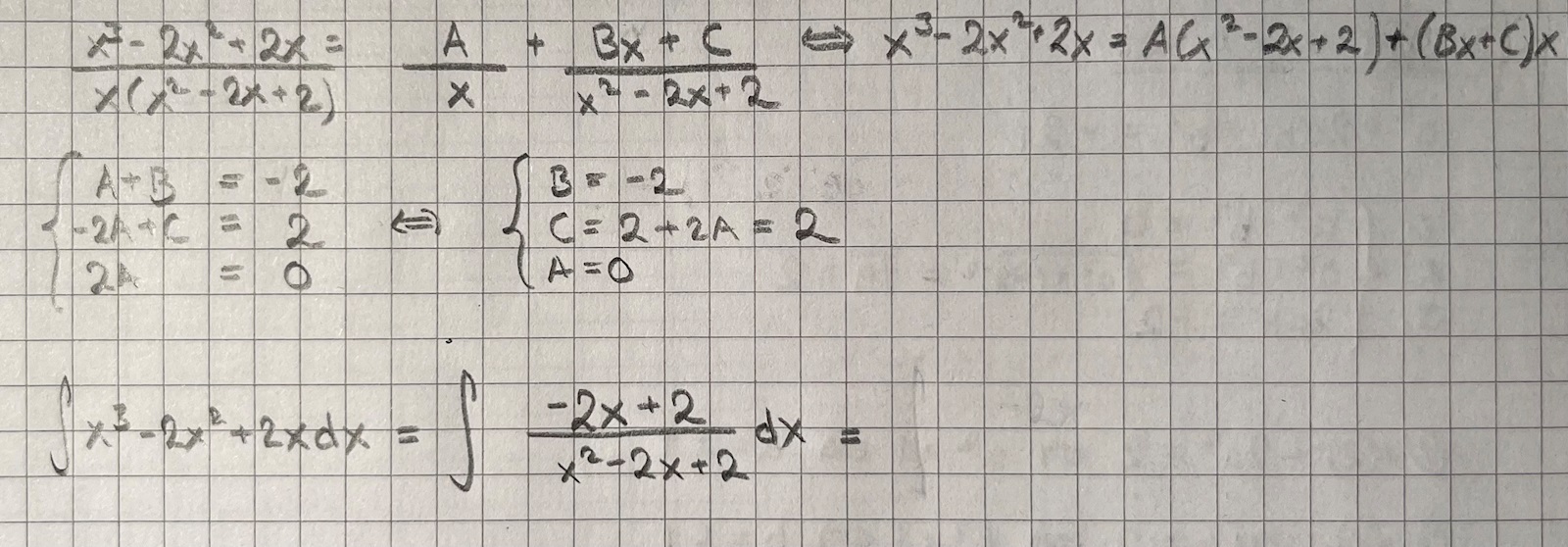
Jag fastnar ändå..! Vet inte hur jag går vidare här? Känns inte som jag fick ut så mycket av partialbråksuppdelningen
Blir det lättare om du delar upp integranden i två termer (med samma nämnare)?
Smaragdalena skrev:Blir det lättare om du delar upp integranden i två termer (med samma nämnare)?
Jag testade, men ser inte direkt något som jag kan göra efter uppdelningen..!
Hur brukar dina integrander se ut efter partialbråksuppdelning? Vad brukar du göra med dem?
Smaragdalena skrev:Hur brukar dina integrander se ut efter partialbråksuppdelning? Vad brukar du göra med dem?

När jag gjort partialbråksuppdelning brukar det, vanligtvis, vara rätt tydligt och enkelt att se vad man kan få ut för primitiver. I denna uppgift var det betydligt svårare i min mening. Men, jag gjorde som du skrev och kan (om jag tänker rätt) få ut en arctan-primitiv av den ena åtminstone :) men är osäker på den första och vad jag kan göra med den integranden



