Beräkna integral
Hej pluggakuten!
Jag ska göra denna uppgift:
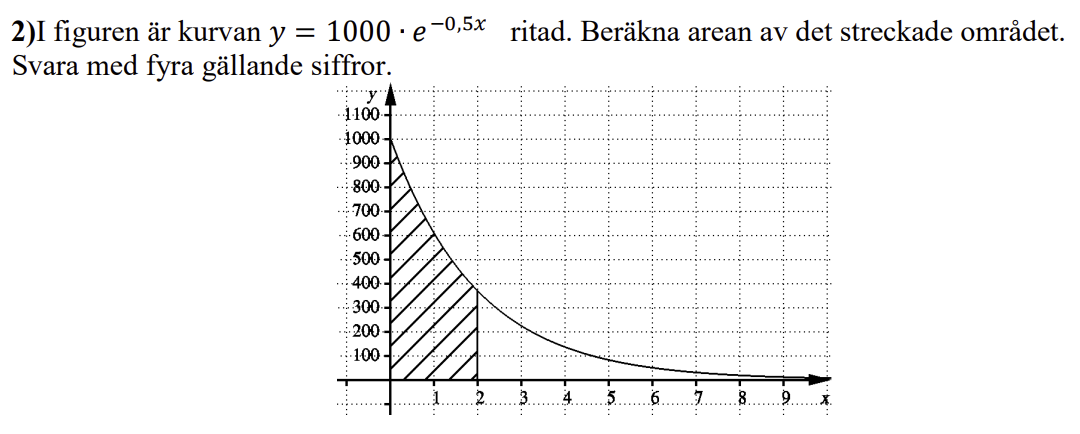
Som svar får jag dock ett negativt tal, vilket omöjligen kan vara rätt!
Jag har skrivit min F som
När jag googlar på andra som har frågat samma sak, så ser jag att svaret är att det inte ska vara något x bakom "1000". Detta förstår jag inte? Enligt formelbladet så leder en funktion "k" till den primitiva funktionen "kx (+C)". Varför gäller inte detta i det här fallet?
Talet 1000 är en faktor, inte en term.
Eftersom derivatan av k•f(x) är k•f'(x) så är en primitiv funktion till k•f(x) lika med k•F(x).
I det här fallet är k = 1000
Aha... Alltså, jag tycker att detta är svårt! För detta går väl faktiskt inte att utläsa från formelbladet, om man endast kollar på raden Funktion k => Primitiv funktion kx+C. För 1000 är väl en konstant k även i mitt exempel.
Förstår dock resonemanget som du beskriver! Så jag jobbar vidare och försöker få in det tankesättet! Tack för hjälpen :)
Hej igen!
Jag insåg nyss att jag dessvärre inte förstår detta fullt ut. Sorry!
I ditt inlägg #2 tolkar jag det som att du använder dig av denna blåmarkerade del i formelbladet och istället går baklänges, för att kunna hitta F/det primitiva uttrycket till funktionen ?

Det jag inte förstår är hur du i så fall visste att du skulle använda dig av just den blåmarkerade raden, och inte den gulmarkerade raden? För uttrycket liknar ju den högra delen i den gulmarkerade raden väldigt mycket. Så där hade jag förmodligen gjort fel i så fall.
ytrewq skrev:Det jag inte förstår är hur du i så fall visste att du skulle använda dig av just den blåmarkerade raden, och inte den gulmarkerade raden? För uttrycket liknar ju den högra delen i den gulmarkerade raden väldigt mycket. Så där hade jag förmodligen gjort fel i så falfall
På den gulmarkerade raden är faktorn framför exponentialuttrycket och faktorn framför x i exponenten båda lika med k. Det är alltså samma konstant k.
Det gör att vi kan använda den gula raden för att direkt bestämma en primitiv funktion till ett uttryck som exempelvis 3*e3x (en primitiv funktion till detta blir alltså e3x).
Så är inte fallet med uttrycket 1000*e-0,5x.
Här är faktorn framför exponentialuttrycket lika med 1000 och faktorn framför x i exponenten lika med -0,5.
Det gör att vi inte enbart kan använda den gula raden för att bestämma en primitiv funktion till 1000*e-0,5x.
I see! Då förstår jag, tack för svaret! :)
Vad bra.
Generellt sett så är ett bra tips för att hitta en primitiv funktion till en funktion f(x) att upprepa följande tills jämförelsen stämmer:
- Gissa en primitiv funktion F(x)
- Derivera F(x)
- Jämför derivatan med f(x)
- Är de lika så är du klar
- Modifiera annars gissningen och gå till steg 2.
Fint! Det har jag glömt bort att göra faktiskt. Det ska jag tänka på till nationella provet - bra att kunna stämma av ifall man har hittat rätt primitiva funktion!
Tack för tipset! :)
ytrewq skrev:Fint! Det har jag glömt bort att göra faktiskt. Det ska jag tänka på till nationella provet - bra att kunna stämma av ifall man har hittat rätt primitiva funktion!
Ja, det bör du alltid göra.
På samma sätt som du
- alltid bör multiplicera ihop faktorerna I ditt förslag på faktorisering för att se att den var korrekt
- alltid bör sätta in dina förslag på lösningar till en ekvation i ursprungsekvationen för att se att den stämmer.
- alltid bör pröva med ett par enkla värden för att se om en förenkling verkar stämma.
Tack Yngve! Jag ska se till att ha detta i åtanke under det nationella provet :D


