beräkna integral
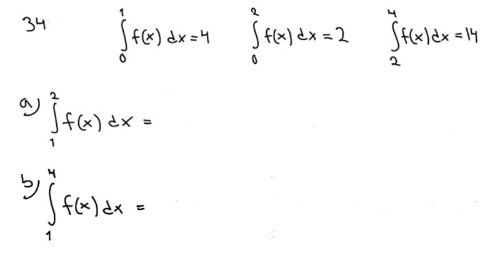
Kan någon hjälpa mig på traven?
Man ska beräkna integralen för a och b genom mha de tre integralerna givna där uppe.
Hej.
Du kan utnyttja att
Ja,
(Låt oss döpa de tre första givna integralerna till a,b,c i den ordning de kommer)
Alltså är de två första, (a,b) lämpliga.
Vi vill i första uppgiften ha integralen med gränserna 1 och 2, men de integralerna ovan (a,b) inkluderar även 0. Hur tänker man då?
Använd formeln som Yngve gav dig. Vilka värden på a, b och c kan du ha för att bestämma dina integraler?
Ja, jag håller med om att man kan utnyttja formeln Yngve föreslog. Men vi vill ha gränserna för 1 och 2, men de integralerna ovan ger för gränserna 0-1 och 0-2, alltså inkluderar de 0, vilket vi inte vill ha i integralen i a-uppgiften (den första uppgiften).
Så jag undrade bara hur vi kunde räkna bort den?
naturnatur1 skrev:Så jag undrade bara hur vi kunde räkna bort den?
Vi har intervallen [0,1], [0,2] och [0,4] att utgå från.
I a-uppgiften är vi ute efter intervallet [1,2]. Är du med på att [1,2] = [0,2] - [0,1]?
Om inte, försök att illustrera dessa tre intervall med hjälp av en tallinje och visa din illustration.
Tillägg: 4 nov 2023 11:33
Första meningens sista intervall blev fel, det ska stå [0,1], [0,2] och [2,4].
Tack Soderstrom för påpekandet.
Yngve skrev:
Är du med på att [1,2] = [0,2] - [0,1]?
Helt ärligt, nej.
Om inte, försök att illustrera dessa tre intervall med hjälp av en tallinje och visa din illustration.
Hur menar du att jag ska göra med tallinjen? Tack på förhand
Markera intervallen i en tallinje.
Du beräknar först arean under kurvan för intervallet [0,2].
Därefter subtraherar du detta med arean under kurvan för intervallet [0,1].
Då får du arean under kurvan för intervallet [1,2]
Okej, tack, 2-4, alltså blir det -2 på a).
På b, är tanken att jag ska använda enbart de övre eller får jag använda även den från a uppgiften?
naturnatur1 skrev:Okej, tack, 2-4, alltså blir det -2 på a).
På b, är tanken att jag ska använda enbart de övre eller får jag använda även den från a uppgiften?
Eftersom att lösningen på (a) uppgiften kan härledas från de övre räcker det med att du använder de övre :)
Dock kommer det förmodligen att krävas en term mindre genom att använda lösningen för (a).
Tillägg: 4 nov 2023 13:42
Du får alltså använda lösningen för (a), eftersom att du i (a) uppgiften härlett den från de övre.
Detta rekommenderas förmodligen.
naturnatur1 skrev:
På b, är tanken att jag ska använda enbart de övre eller får jag använda även den från a uppgiften?
Spelar ingen roll. Klarar du av att lösa uppgiften utan svaret i a) så är det väl bra? Testa.
Om man får använda den med a så har jag inga problem, så (14) + (-2) = 12
Men om man enbart får använda de övre vill jag även kunna se lösningen på. Jag ritade intervallen i en tallinje men tror jag behöver lite tips.
Lämpliga att använda skulle jag tro är [2,4] respektive [0,1] ? Vilket dock motsäger det ursprungliga svaret jag fick.
Igen. Rita en tallinje och kontrollera om dina beräkningar verkligen stämmer.
Jag har ritat. Men jag kommer inte på någon metod där vi direkt kan uttnytja någon av de 3 ovanstående integralerna, utan att utgå från den i a-uppgiften (ta samma steg för att komma fram dit).
Tillägg: 4 nov 2023 14:18

GUL- den vi söker
RÖD- [2,4], sista givna integralen.
GRÖN - sträcka som saknas.
Är inte grönt område ?
Soderstrom skrev:Är inte grönt område ?
Ja, det vill säga det man beräknade i a uppgiften. (-2)
Ja. Utnyttja det.
Soderstrom skrev:Ja. Utnyttja det.
Ja, jag gjorde det i #14, vilket jag är med på. Trodde det fanns ytterligare en väg, så därför jag frågade.
Du kan beräkna integralerna i både a) och b) på oändligt många sätt, men givet informationen i uppgiften är vi begränsade :)
Då är jag med.
Tack för hjälpen alla i denna tråd!




