Beräkna höjden ljuskälla maximera ljusintensiteten
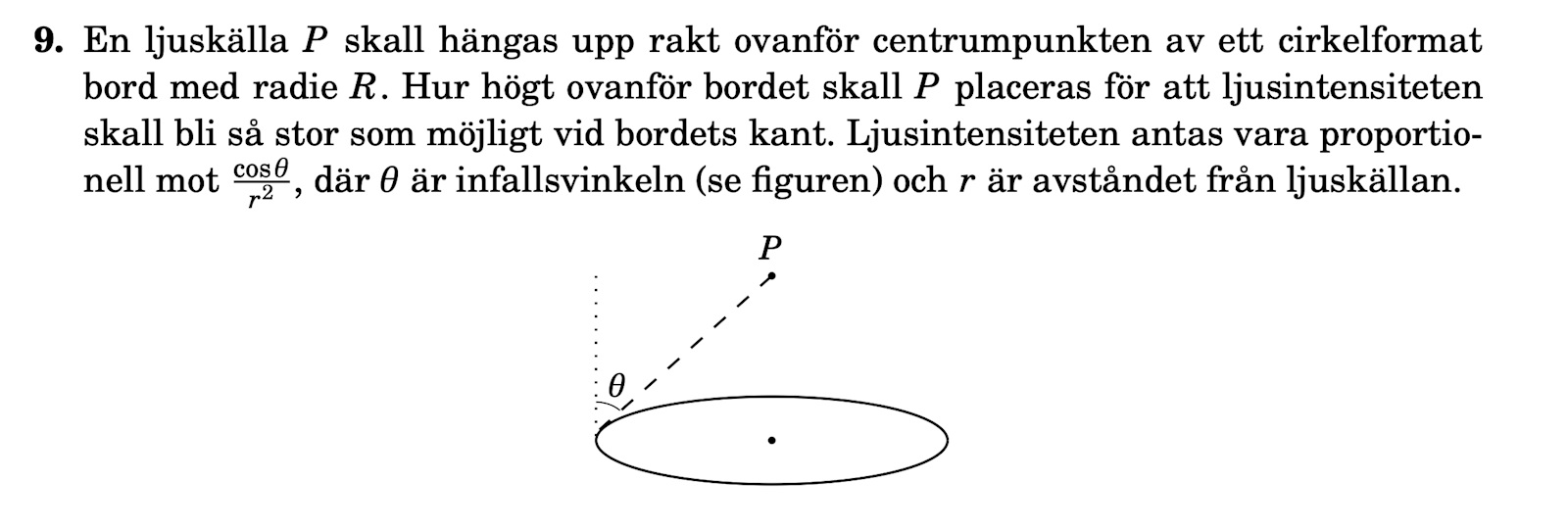
En ljuskälla P skall hängas upp rakt ovanför centrumpunkten av ett cirkelformat
bord med radie R. Hur högt ovanför bordet skall P placeras för att ljusintensiteten
skall bli så stor som möjligt vid bordets kant. Ljusintensiteten antas vara proportionell mot cosθ, där θ är infallsvinkeln (se figuren) och r är avståndet från ljuskällan.
Jag har försökt lösa denna uppgiften genom att sätta tan x=r/R och sedan löst ut r=Rtanx som jag kvadrerat och satt i nämnaren på cosx/r2, förenklat och sedan deriverat och då får jag en derivata som ser ut såhär men jag verkar missa något. Använde tan eftersom jag vill ha med R i mitt uttryck
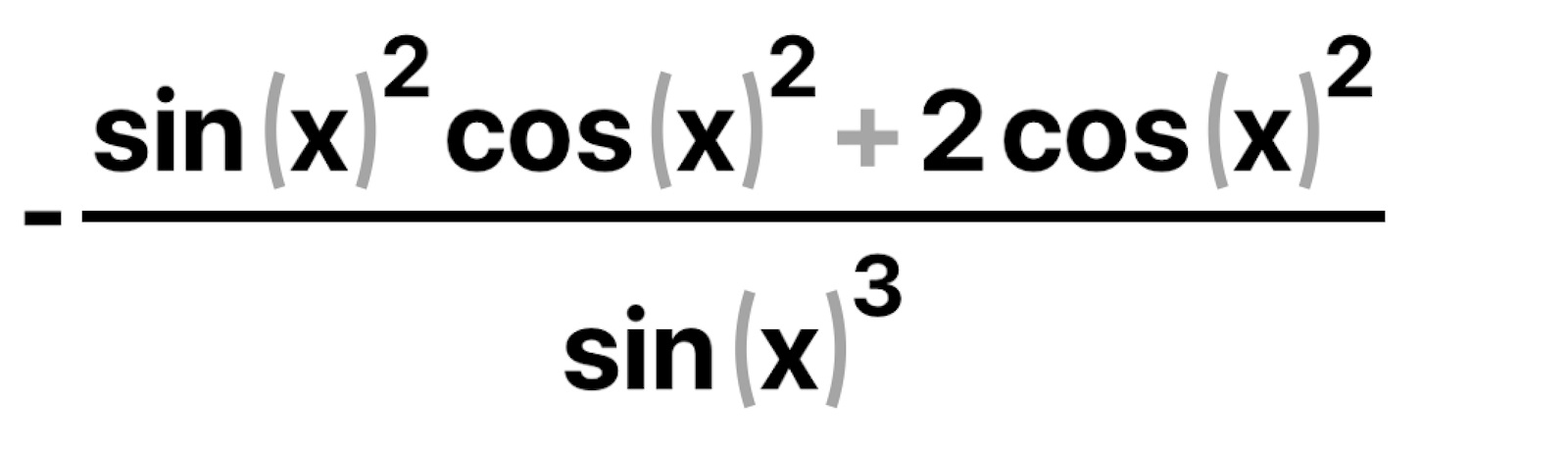
Har också funderat ifall jag ska kombinera Pythagoras sats eller använda rätvinkliga sambanden (tan, sin, cos för att hitta ett samband. Finns en liknande uppgift
Som i princip är identisk men jag löser inte det. När jag väl får rätt uttryck så är det ju bara att se när värdet (vinkeln) blir så stor som möjligt.
I(x) = k cos(x)/r^2
men R=rsin(x) så
I(x) = k/R^2 cos(x)sin^2(x)
Maximera cos(x)sin^2(x)
Eftersom du söker rcos(x) kan du även maximera u(1-u^2) varpå ditt svar är r*u_max.
Trinity2 skrev:I(x) = k cos(x)/r^2
men R=rsin(x) så
I(x) = k/R^2 cos(x)sin^2(x)
Maximera cos(x)sin^2(x)
Eftersom du söker rcos(x) kan du även maximera u(1-u^2) varpå ditt svar är r*u_max.
Kan det då vara så att jag tänkt fel kring vad som är r? För då klarnar det verkligen! Förstår dock inte vad du menar med u(1-u^2) men får fram rätt svar nu!
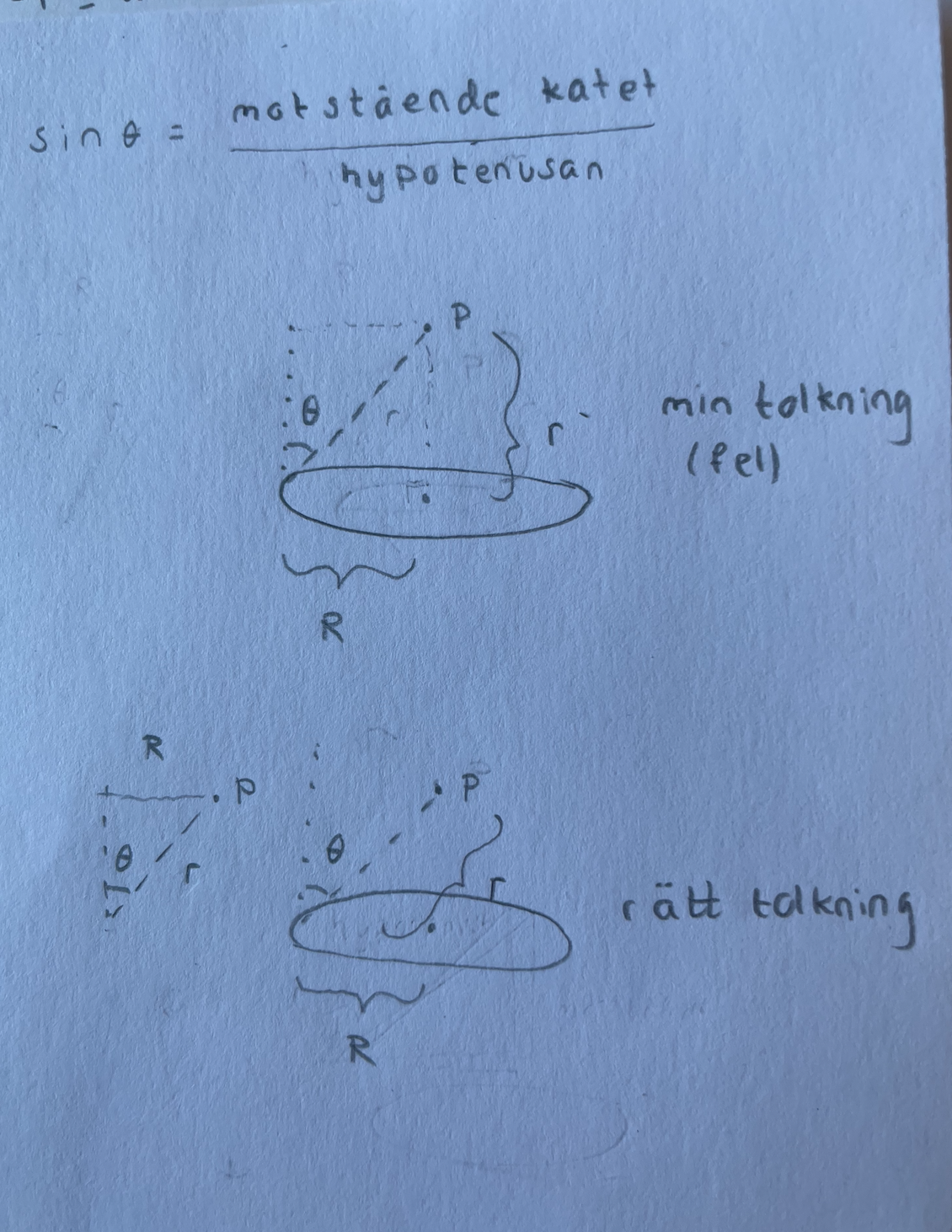
I det ena fallet räknar man med vinkeln mellan ljusstrålen och bordet, i det andra fallet mellan ljusstrålen och normalen mot bordsytan.
Smaragdalena skrev:I det ena fallet räknar man med vinkeln mellan ljusstrålen och bordet, i det andra fallet mellan ljusstrålen och normalen mot bordsytan.
Vill du förklara med en bild? Har svårt att föreställa mig var normalen skulle vara.
Du har redan en bild som visar det, i ditt förstainlägg uppgift 9. Normalen är den prickade linjen, vinkelrät mot bordsytan.
Jag förstår fortfarande inte vilka trigonometriska samband ni ställer upp för att få cos(x)sin^2(x). Jag har ju motstående- och närliggande katet men jag kan ju inte använda varken sinus eller cosinus utan ett samband för hypotenusan.
Om du vet vinkeln v och antingen a eller r kan du beräkna h:
h = r cosv = a sinv i den vänstra bilden, h = r sinv = a cosv i den högra bilden (kallar vinkeln v för det är enklare att skriva).
Du kan också använda Pythagoras sats: a2+r2 = h2
Tack det du skrivit underlättar verkligen! Så om jag förstår allt rätt nu så är det höjden de vill att man ska beräkna som är hypotenusan?
Nej, höjden skall mätas vinkelrätt mot bordsskivan.
Fortfarande så blir jag så extremt förvirrad eftersom cosv=närliggande katet/hypotenusan, därför förstår jag inte hur du kan sätta ut de sambanden.
Om du vet både bordsskivans radie och avståndet upp till lampan så kan du beräkna vinkeln med hjälp av tangens. Sedan kan du använda sinus eller cosinus för att beräkna hypotenusan, eller Pythagoras sats direkt om du hellre vill det.
