Beräkna Fouriertransformen

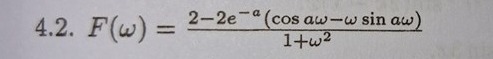
De förlänger för att få reell nämnare, så att nämnaren blir (1-w²) för båda uttrycken.

Förläng med det komplexa talets konjugat för de två termerna.

Bedinsis skrev:

De förlänger för att få reell nämnare, så att nämnaren blir (1-w²) för båda uttrycken.

Förläng med det komplexa talets konjugat för de två termerna.

Okej! De förlänger alltså med konjugatet. Men det är inte ett måste eller? Man kan svara så som sista raden i lösningen?

Edit: de skriver även om täljaren med Eulers formel.

Generellt sett bör en lösning som kan skrivas utom imaginära termer skrivas utan imaginära termer.

Bedinsis skrev:

Generellt sett bör en lösning som kan skrivas utom imaginära termer skrivas utan imaginära termer.

Insåg nu att jag inte kommer vidare, även om jag förlänger med konjugatet;

$\displaystyle=...=\frac{(1+iw)(1-e^{a(iw-1)})+  (1-iw)(1-e^{a(-1-iw)})}{1+w^2}$

Ser inte vad som ska faktoriseras! 

Har du prövat att utveckla parenteserna? Jag skulle för enkelhetens skull skriva om med:

$z= 1+i w$

$z*=1-iw$

Edit: Å andra sidan, om du är mindre van vid komplex algebra är det nog ingen bra idé. Men kom ihåg att:

$2\cdot\cos(z) = e^{iz}+e^{-iz}$

$2i\cdot \sin(z)= e^{iz}-e^{-iz}$

För något komplext tal $z \in \mathbb{C}$.

Tja, du har ju i*w*1 i första termen och -i*w*1 i andra termen. Dessa borde du kunna ta bort om du utvecklar parenteserna.