Beräkna en punkt tangenten till en parabel slår.
Figuren visar en parabelformad väg sedd från ovan.
En bil startar i punkten (-100,100) enligt figuren. Viktor står i punkten (100,50)
Bestäm koordinaterna för den punkt på vägen där bilens strålkastare är riktade rakt mot Viktor.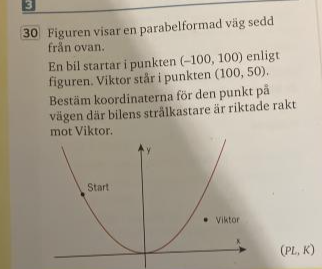 Min felaktiga lösning
Min felaktiga lösning
Parabeln slår origo och saknar då både b och c term.
Alltså y = ax^2
det visar sig vara f(x) =
Vi vill då ha tangenten som träffar viktors punkt.
Tangentens lutning är derivatan
där a är någon punkt. genom att lägga in x=a och f(a) för y kan man få m-värdet
tangentens ekvation är då
och här tänker jag att man kan bara sätta in y = 50 och x = 100 för att få värdet på a då denna linjära funktion slår punkten (100,50)
Detta har inga lösningar och jag är rätt så förvirrad. Jag vet att ekvationen för tangenten stämmer, jag har kollat det och jag vet att funktionen är rätt. Så det som är fel är när jag lägger in x = 100 och y = 50. Här har jag dock fastnat och vet inte vad den korrekta fortsättningen är.
Det blir 5000 = 200a - a2 på näst sista raden.
Du kanske kan göra lösningen lite tydligare.
"Tangentens lutning är derivatan", derivatan är x/50, m kommer senare.
a är x-värdet för någon punkt på kurvan.
Du behöver nog kommunicera bättre än det du skrev i tråden om du vill få full pott, då den uppgift testar bland annat kommunikationsförmågan.
Louis skrev:Det blir 5000 = 200a - a2 på näst sista raden.
Du kanske kan göra lösningen lite tydligare.
"Tangentens lutning är derivatan", derivatan är x/50, m kommer senare.
a är x-värdet för någon punkt på kurvan.
Fan vilket dumt misstag jag gjorde där
Soderstrom skrev:Du behöver nog kommunicera bättre än det du skrev i tråden om du vill få full pott, då den uppgift testar bland annat kommunikationsförmågan.
Jag vet det. Jag gillar inte att skriva in uträkningar i text på datorn dock och förkortar det så mycket som möjligt


