Beräkna derivatan för funktionen f(x)

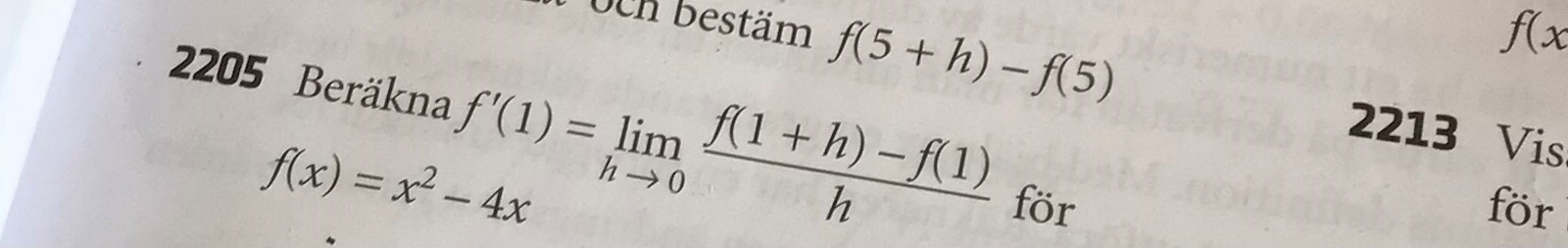
Så här har jag tänkt kring frågan

Nästan! Det skall inte vara vara 4x som andra term i täljaren på första raden, det skall vara 4(x+h).

Smaragdalena skrev:

Nästan! Det skall inte vara vara 4x som andra term i täljaren på första raden, det skall vara 4(x+h).

Kan du färgnarkera vart nånstans jag gjorde fel ?

Du skall ju sätta in x+h på båda de ställen i f(x) där det står x.

Jag förstår inte hur du menar ?

Kan du visa vad det korrekta är ?

Om f(x) = x²-4x så är f(x+h) = (x+h)²+4(x+h).

varför blev mitt inlägg fel ?

Det känns som att det ännu inte riktigt har landat hos dig hur f(x+h) ser ut om du känner till hur f(x) ser ut.

Jag föreslår återigen att du gör en "faktaruta" där du skriver dels skriver uttrycket för f(x), dels uttrycket för f(x+h).

Sedan är jag övertygat om att din envisa vägran att svara på mina frågor  t.ex. dessa, är en bov i dramat. 

Yngve jag tittade på inlägget du hänvisade. Men, tar dessvärre längre tid för mig att begripa det här eftersom det är nytt. 

Jag kanske kan låta som envis ibland, men det oftast för att jag har svårt att begripa saker på meddeland här på PA än räknestuga där vi kan disskutera saker (fysiskt).

Nu ska jag vara tydlig.

Om du vill ha hjälp här på Pluggakuten så bör du anstränga dig att svara på våra frågor och följa våra tips.

Om du inte förstår frågorna så ska du fråga och be oss förklara vad det är vi vill att du ska göra.

Om du inte förstår tipsen så ska du fråga och be oss förklara hur vi vill att du ska följa tipsen.

Om du varken bsvarar frågor, följer tips eller ber om förklaringar så riskerar du att framstå som nonchalant och otacksam.

=====

Orsaken till att vi ställer frågor och ger tips är inte att förvirra dig. Det är inte heller så att frågorna är ovidkommande.

Istället är det så att frågorna och tipsen är avsedda att hjälpa dig att snabbare förstå och lära dig begreppen och sambanden.

=======

Så jag rekommenderar dig nu att börja svara på frågor eller be om förtydligande. Det kommer att hjälpa dig att lära dig snabbare.

=======

Är det verkligen så att du inte förstår de nio frågorna jag ställde i den andra tråden?

Arup skrev:

Yngve jag tittade på inlägget du hänvisade. Men, tar dessvärre längre tid för mig att begripa det här eftersom det är nytt. 

Vad menar du med detta?

Jag förstår inte vad du menar Mr. P  jag var väl ganska tydlig ?

Det tycker jag inte. Att det är ett nytt ämne och tar därför längre tid att begripa har väl inget att göra med varför du inte svarar på frågorna? 

Ok du har rätt.

Arup skrev:

varför blev mitt inlägg fel ?

Har du fått svar på denna fråga?

Yngve skrev:

Arup skrev:

varför blev mitt inlägg fel ?

Har du fått svar på denna fråga?

delvis eller jag är fortfarande osäker varför det skulle vara så här: 

Om f(x) = x²-4x så är f(x+h) = (x+h)²+4(x+h). (som Smaragdalena påpekade)

istället för ${(x+h)}^2-4x.$

OK vi försöker så här:

Utgå från f(x) = x²-4x

Du vill nu ta fram ett uttryck för f(x+h).

Gör då som i den andra tråden, att du tillfälligt sätter (substituerar) y = x+h.

Ta sedan fram uttrycket för f(y):

f(y) = y²-4y

Byt nu tillbaka från y till x+h:

f(x+h) = (x+h)²-4(x+h)

Blev det tydligare då?

yngve borde det inte vara 4 vara posstiv ? eftersom -(-)=+

Arup skrev:

yngve borde det inte vara 4 vara posstiv ? eftersom -(-)=+

Nej, varifrån får du det andra minustecknet?

Ta gärna en screenshot eller bild med mobilen och visa.

f(x+h)-f(x)

(x+h)^2-(-4)(x+h)

Arup skrev:

f(x+h)-f(x)

(x+h)^2-(-4)(x+h)

Är du med på följande?

• f(x) = x²-4x
• f(x+h) = (x+h)²-4(x+h)

ok, är det för att det är en funktion dvs f(x+h) ?

Ja, f är en funktion 

Funktionsuttrycket är

f(x) = x²-4x

då måste jag ha blandat de två funktionerna f(x) och f(x+h)

Arup skrev:

då måste jag ha blandat de två funktionerna f(x) och f(x+h)

... och det är just därför jag vill att du ska göra en "faktaruta", för att slippa hålla så mycket saker I huvudet samtidigt.

Det minskar risken att blanda ihop uttrycken.

Säg till om du inte förstår vad jag skriver, om du inte har klart för dig vad en faktaruta är, vad den i det hör fallet lämpligen bör innehålla eller hur den ska användas.

Eller om det är något annat som är otydligt/oklart.

min fakta ruta ser ut något i den stilen kommenter gärna om det ser bra ut så kan jag utföra beräkningen :

$$\begin{gathered} \bullet f\left(x\right)=x^2-4x \\ \bullet f(x+h)={(x+h)}^2 \\ \bullet \mathrm{f}(\mathrm{x}+\mathrm{h})-\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{h}\to 0}{\lim }\frac{{(\mathrm{x}+\mathrm{h})}^2-4(\mathrm{x}+\mathrm{h})-({\mathrm{x}}^2-4\mathrm{x})}{\mathrm{h}} \end{gathered}$$

Arup skrev:

min fakta ruta ser ut något i den stilen kommenter gärna om det ser bra ut så kan jag utföra beräkningen :

$$\begin{gathered} \bullet f\left(x\right)=x^2-4x \\ \bullet f(x+h)={(x+h)}^2 \\ \bullet \mathrm{f}(\mathrm{x}+\mathrm{h})-\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{h}\to 0}{\lim }\frac{{(\mathrm{x}+\mathrm{h})}^2-4(\mathrm{x}+\mathrm{h})-({\mathrm{x}}^2-4\mathrm{x})}{\mathrm{h}} \end{gathered}$$

Första raden ser bra ut.

På andra raden har du glömt att skriva ut termen -4(x+h). Dessutom är det bra om du förenklar uttrycket för f(x+h) redan här, innan du ska använda det i ett senare skede.

Tredje raden stämmer inte alls:

Till vänster om likhetstecknet har du skrivit f(x+h)-f(x), dvs täljaren I differenskvoten.

Till höger om likhetstecknet har du skrivit ett gränsvärde (som i och för sig mycket riktigt är det eftersökta uttrycket för ddrivatan), men det är inte identiskt med vänsterledet.

hur skulle rätt uppställning vara ?

Förslagsvis så här:

$f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}$.

==== Faktaruta ====

$f(x)=x^2-4x$

$f(x+h)=(x+h)^2-4(x+h)=$

$=x^2+2hx+h^2-4x-4h$

================

Vi tittar nu endast på differenskvotens täljare, dvs $f(x+h)-f(x)$.

Vi kan sätta ihop detta uttryck med hjälp av komponenter från faktarutan:

$f(x+h)-f(x)=$

$=(x^2+2hx+h^2-4x-4h)-(x^2-4x)=$

$=x^2+2hx+h^2-4x-4h-x^2+4x=$

$=2hx+h^2-4h=h(2x+h-4)$

Nu ersätter vi täljaren i derivatans definition med detta förenklade uttryck och vi får då

$f'(x)=\lim_{h\rightarrow0}\frac{h(2x+h-4)}{h}=$

$\lim_{h\rightarrow0}(2x+h-4)=2x-4$

Förstod du alla steg i det lösningsförslaget?

Fråga gärna om det är något som är oklart.

Yngve skrev:

Förstod du alla steg i det lösningsförslaget?

Fråga gärna om det är något som är oklart.

vad menar du med "differenskvoten" ?

En differenskvot är en kvot mellan två differenser.

I det här fallet är.den ena differensen $f(x+h)-f(x)$ och den andra $(x+h)-x$, dvs $h$.

Differenskvoten är alltså $\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}$

Läs gärna mer här.

är det samma sak som riktningkoefficenten för två punkter dvs:

k=$\frac{y_2-y_1}{x_2-x_1}$

Bra att du ser likheten!

Den formeln för en rät linjes riktningskoefficient är ett annat exempel på en differenskvot.

har du möjlighet att färgmarkera faktarutan? Eftersom jag håller på att skriva ditt svar på inlägg #31 på papper för extra träning.

nevermind