Beräkna den frigjorda energin
Hej! Jag undrar en sak om denna uppgift: "Beräkna den frigjorda energin för β+-sönderfall av Kalium-40."
Min boks lösningsförslag:

Mitt problem är, jag förstår inte varför det går att räkna bort elektronernas massa från nuklidmassan hos K-40 och Ar-40. Jag förstår att syftet med att göra detta är att få fram enbart atomkärnornas massor. Men det finns väl massdefekt hos elektronerna, som gör att elektronerna väger olika mycket i de olika atomerna? Så hur kan man subtrahera samma värde på elektronmassan från båda dessa atomer?
Det är lite lågt ja, K-40 sönderfall kan ge en gamma på 1,46 MeV, och det är för beta-plus elektroninfångning.
Om man slår upp K-40 i isotoptabellen ser man att Q-värde för ß+ sönderfall är 1,505 MeV.
Det stämmer med bokens facit om man adderar två elektroner. 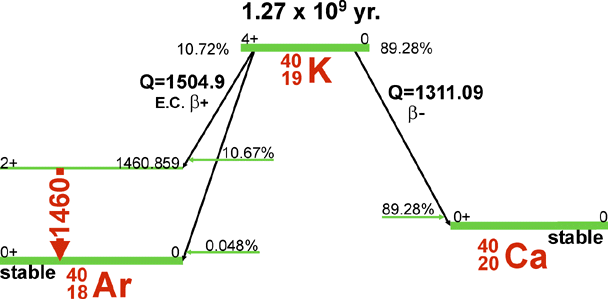
Pieter Kuiper skrev:Det är lite lågt ja, K-40 sönderfall kan ge en gamma på 1,46 MeV, och det är för beta-plus.
Om man slår upp K-40 i isotoptabellen ser man att Q-värde för ß+ sönderfall är 1,505 MeV.
Det stämmer med bokens facit om man adderar två elektroner.
Jag hänger tyvärr inte med på något av din förklaring. Det är för hög nivå för mig. Skulle du kunna förklara det på gymnasienivå? Tack.
Boken försöker räkna ut räkna ut hur mycket massa blir energi. Det kan vara lite svårt att veta vad det är som står i tabellerna men det är vanligtvis atommassor inklusive alla elektroner av en neutral atom.
Men hur man än gör, om det försvinner bara 0,483 MeV i massa, hur kan man då få en gamma-foton med 1460 eV?
K-40 kan sönderfalla åt två håll: Ca-40 eller Ar-40. Exemplet handlar om Ar-40 och där har riktiga kärnfysiker räknat ut att Q-värdet är 1504,9 keV. Det kan ske på två sätt: sända ut en positron eller EC (electron capture, elektroninfångning där en elektron slukas av kärnan). Om det blir emission av en positron annihilerar den sedan och ger två gamma på 511 keV var.
Här har boken räknat att positronen är kvar. Så det är skillnaden: när den annihileras blir reaktionen:
40K → 40Ar + 2*0,511 MeV + 0,483 MeV.
Bara när det är elektroninfångning kan det bli en 1460 keV gammafoton.
Pieter Kuiper skrev:Boken försöker räkna ut räkna ut hur mycket massa blir energi. Det kan vara lite svårt att veta vad det är som står i tabellerna men det är vanligtvis atommassor inklusive alla elektroner av en neutral atom.
Men hur man än gör, om det försvinner bara 0,483 MeV i massa, hur kan man då få en gamma-foton med 1460 eV?
K-40 kan sönderfalla åt två håll: Ca-40 eller Ar-40. Exemplet handlar om Ar-40 och där har riktiga kärnfysiker räknat ut att Q-värdet är 1504,9 keV. Det kan ske på två sätt: sända ut en positron eller EC (electron capture, elektroninfångning där en elektron slukas av kärnan). Om det blir emission av en positron annihilerar den sedan och ger två gamma på 511 keV var.
Här har boken räknat att positronen är kvar. Så det är skillnaden: när den annihileras blir reaktionen:
40K → 40Ar + 2*0,511 MeV + 0,483 MeV.
Bara när det är elektroninfångning kan det bli en 1460 keV gammafoton.
Ok, nu var det några dagar sedan jag skapade tråden. Men jag tror tyvärr jag var otydlig, så du har nog inte svarat på det jag ville veta. Min riktiga fråga var: "Finns det massdefekt för elektroner?" Jag undrar detta eftersom nukleoner ju har massdefekt; deras massa är större i fri form än i bunden form. Det förefaller mig därför vara rimligt att elektroner inte heller avviker från denna regel, d.v.s. att även elektroner har massdefekt.
Om svaret på min fråga är "ja, det finns massdefekt för elektroner", så antar jag att elektronmassorna måste variera beroende på vilket ämne elektronerna finns i. Det är detta som gör mig förvirrad. När min bok räknar ut massor för olika ämnens atomkärnor så subtraherar man elektronmassorna från nuklidmassan. Oavsett vilket ämne det handlar om så subtraherar man alltid samma värde på elektronmassa. Men då är ju problemet att elektronmassan inte har samma värde i alla ämnen; det finns ju massdefekt. Så jag undrar: varför säger min bok att man ska subtrahera samma värde på elektronmassan oavsett vilket ämne det är?
Hoppas jag var lite tydligare nu.
Ah! Det har jag aldrig funderat på, men det är en bra fråga.
För kalium är det ingen stor effekt. Bindningsenergi i K-skalet är typ 3 keV, mycket mindre än vilomassan på 511 keV.
I tyngre grundämnen blir det annorlunda, i uranium är bindningsenergi för K-skalet drygt 100 keV. Men även där är det inte så viktigt att ta med i beräkningar. Vid radioaktivt sönderfall (alfa eller beta) blir det igen en atom med nästan lika stora bindningsenergier. Så allt detta ger bara små skillnader. Det är nog mätbart om man är mycket noga, men det syns bara i decimaler som inte är med i vanliga tabeller.
Pieter Kuiper skrev:Ah! Det har jag aldrig funderat på, men det är en bra fråga.
För kalium är det ingen stor effekt. Bindningsenergi i K-skalet är typ 3 keV, mycket mindre än vilomassan på 511 keV.
I tyngre grundämnen blir det annorlunda, i uranium är bindningsenergi för K-skalet drygt 100 keV. Men även där är det inte så viktigt att ta med i beräkningar. Vid radioaktivt sönderfall (alfa eller beta) blir det igen en atom med nästan lika stora bindningsenergier. Så allt detta ger bara små skillnader. Det är nog mätbart om man är mycket noga, men det syns bara i decimaler som inte är med i vanliga tabeller.
Jag godtar det som svar :) Tack.


