Beräkna covariansen för beroende variabler?
Hej! Jag försökte lösa denna uppgift men fastnade på hur jag skulle berökna covariansen då variablerna är beroende? nu nör jag ser facit förstår jag inte heller hur de kommer fram till att cov(xi1,xi2) =4 ?

Min lösning (ej fullständig)

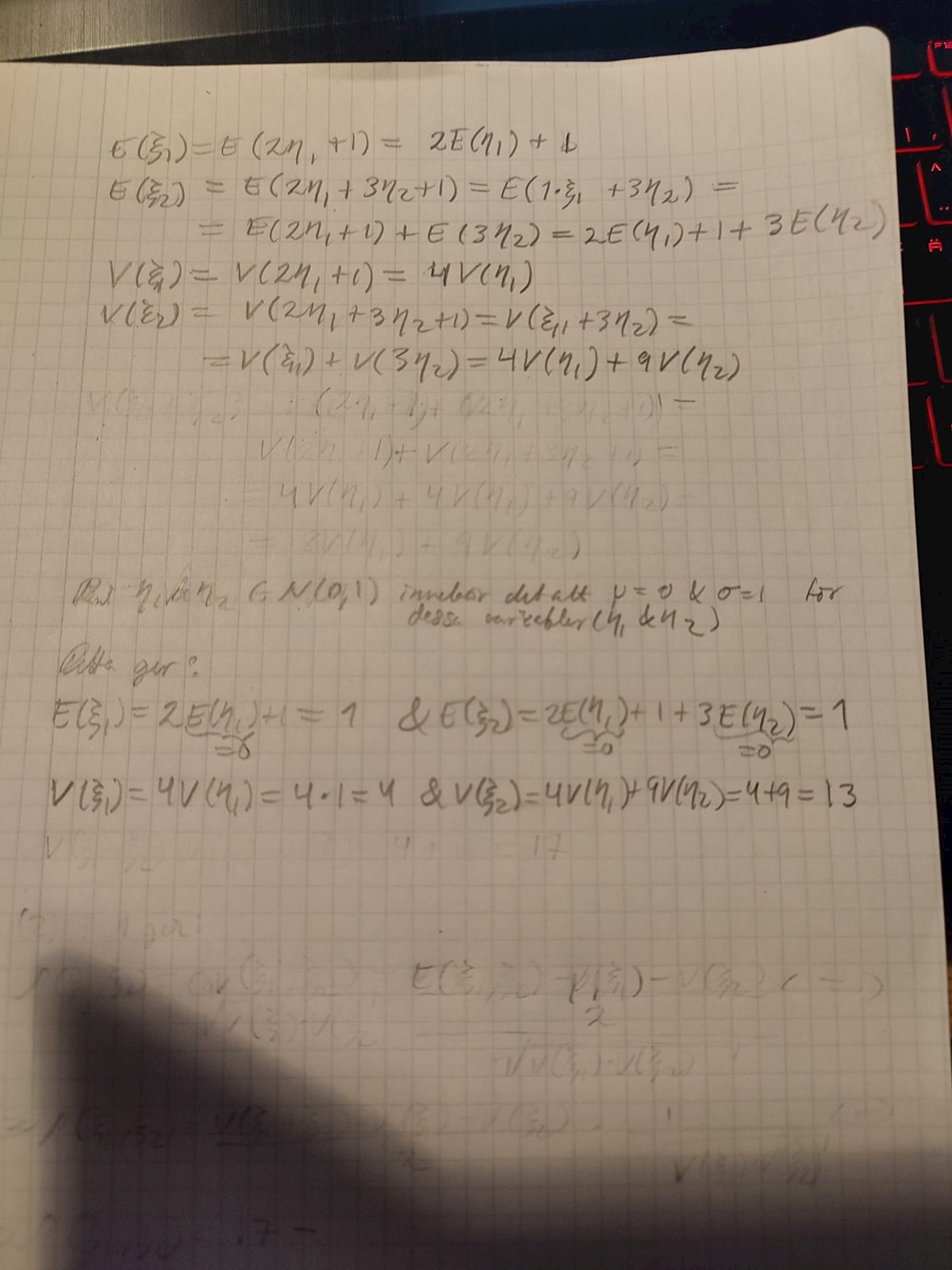
Tack på förhand!
Det finns flera olika metoder att bestämma covariansen på.
Lösningsförslaget beräknar Cov(xi1,xi2) genom att uttrycka xi1 och xi2 i eta (dessa uttryck har du skrivit upp ovanför). Därefter kan vi utnyttja det faktum att covariansen är en linjär operator, dvs Cov(aX+Y,Z) = a*Cov(X,Z)+Cov(Y,Z) för stok. variabler X,Y,Z och ett deterministiskt tal a.
Det går även bra att använda den satsen du skrivit upp. Då behöver du bestämma E[xi1xi2]. Börja med att uttrycka xi1 och xi2 i uttrycken som innehåller eta och bestäm sedan denna produkt. Sedan använder du dig reglerna för väntevärdet.
Calle_K skrev:Det finns flera olika metoder att bestämma covariansen på.
Lösningsförslaget beräknar Cov(xi1,xi2) genom att uttrycka xi1 och xi2 i eta (dessa uttryck har du skrivit upp ovanför). Därefter kan vi utnyttja det faktum att covariansen är en linjär operator, dvs Cov(aX+Y,Z) = a*Cov(X,Z)+Cov(Y,Z) för stok. variabler X,Y,Z och ett deterministiskt tal a.
Det går även bra att använda den satsen du skrivit upp. Då behöver du bestämma E[xi1xi2]. Börja med att uttrycka xi1 och xi2 i uttrycken som innehåller eta och bestäm sedan denna produkt. Sedan använder du dig reglerna för väntevärdet.
Tack för svar!
Jag förstår dock inte hur de kommer fram till att det till slut bara blir 4?
På den andra metoden blir jag också osäker hur jag ska fortsätta? Jag får att:
FInns det någon regel på om man har en stokastisk variabel eta som är multiplicerad med sig själv?
Precis vilket steg är det du inte förstår i den första metoden?
Metod 2: Till att börja med kan du använda linjäriteten hos väntevärdet. Därefter kan du uttnyttja samma sats igen, fast applicerat på eta1 och eta2, dvs Cov(eta1,eta2)=E[eta1eta2]-E[eta1]E[eta2]
Calle_K skrev:Precis vilket steg är det du inte förstår i den första metoden?
Metod 2: Till att börja med kan du använda linjäriteten hos väntevärdet. Därefter kan du uttnyttja samma sats igen, fast applicerat på eta1 och eta2, dvs Cov(eta1,eta2)=E[eta1eta2]-E[eta1]E[eta2]
Jag ser inte riktigt vad de skrivit i metod 1? de skriver att Cov(xi1,xi2) = cov(2eta1+1,2eta1+3eta2+1) = 4var(eta1) + 6cov(eta1 ?eta2) . Efter likamedtecknet efter 6cov(...) ser jag inte vad de skrivit? sedan förstår jag inte varför det blir 6cov?
För metod 2, med att använda linjäriteten, menar du att jag ska använda mig av att E(eta1) = E(eta2)=0? för då får jag följande:
E(ξ1,ξ2) = E(2η1+1)(2η1+3η2+1)) =
=E(4η21+6η1η2+4η1+3η2+1) =
=
Detta ger då att Cov(xi1,xi2)= E(xi1xi2) - my1my2 = 1 -1*1 = 0
Vilket inte stämmer:( Vet inte riktigt hur man ska göra?
Metod 1: (Jag använder X och Y istället för eta1 och eta2).
Cov(xi1,xi2) = Cov(2X+1,2X+3Y+1) = {linjäritet hos covariansen} = (2+2)*Cov(X,X)+(2+3)*Cov(X,Y) = 4
Det sista steget följer av att Cov(X,X) = Var(X) = 1 och Cov(X,Y)=0 eftersom att X och Y är oberoende.
Hänger du med på alla steg nu?
Metod 2:
Nästan, men E[XY] är inte lika med E[X]E[Y]
Det stämmer faktiskt att E[XY]=E[X]E[Y] i detta fall eftersom att X och Y är oberoende.
MEN! E[X2] är inte lika med E[X]2, eftersom X är i allra högsta grad beroende med sig själv.
Calle_K skrev:Metod 1: (Jag använder X och Y istället för eta1 och eta2).
Cov(xi1,xi2) = Cov(2X+1,2X+3Y+1) = {linjäritet hos covariansen} = (2+2)*Cov(X,X)+(2+3)*Cov(X,Y) = 4
Det sista steget följer av att Cov(X,X) = Var(X) = 1 och Cov(X,Y)=0 eftersom att X och Y är oberoende.
Hänger du med på alla steg nu?
Metod 2:
Nästan, men E[XY] är inte lika med E[X]E[Y]
Det stämmer faktiskt att E[XY]=E[X]E[Y] i detta fall eftersom att X och Y är oberoende.
MEN! E[X2] är inte lika med E[X]2, eftersom X är i allra högsta grad beroende med sig själv.
Metod 1: NU förstår jag nästan alla steg, detta steg dock:
{linjäritet hos covariansen} = (2+2)*Cov(X,X)+(2+3)*Cov(X,Y)
Innebär det att man om man har två variabler X och Y och konstanter a & b & c så:
Cov(aX, cX + bY) = (a+c)Cov(X,X) + (a+b)Cov(X,Y)?
Alltså att man för varje variabel till höger tar covariansen med varje variabel till höger om komma tecknet och att man adderar konstanterna som finns framför? (Förlåt för dålig beskrivining, vet inte riktigt hur jag ska förklara:()
Metod 2:
Ah okej! Men hur beräknar man då E(x^2)?
Metod 1: NU förstår jag nästan alla steg, detta steg dock:
{linjäritet hos covariansen} = (2+2)*Cov(X,X)+(2+3)*Cov(X,Y)
Innebär det att man om man har två variabler X och Y och konstanter a & b & c så:
Cov(aX, cX + bY) = (a+c)Cov(X,X) + (a+b)Cov(X,Y)?Alltså att man för varje variabel till höger tar covariansen med varje variabel till höger om komma tecknet och att man adderar konstanterna som finns framför? (Förlåt för dålig beskrivining, vet inte riktigt hur jag ska förklara:()
Helt rätt! Linjäriteten innebär alltså att man kan flytta ut summor och multiplikation med skalärer utanför operatorn.
Metod 2:
Ah okej! Men hur beräknar man då E(x^2)?
Du använder samma sats som tidigare, dvs Cov(X,Y)=E[XY]-E[X]E[Y], fast du använder du Y=X.
Kom ihåg att Cov(X,X)=Var(X)
Calle_K skrev:Metod 1: NU förstår jag nästan alla steg, detta steg dock:
{linjäritet hos covariansen} = (2+2)*Cov(X,X)+(2+3)*Cov(X,Y)
Innebär det att man om man har två variabler X och Y och konstanter a & b & c så:
Cov(aX, cX + bY) = (a+c)Cov(X,X) + (a+b)Cov(X,Y)?Alltså att man för varje variabel till höger tar covariansen med varje variabel till höger om komma tecknet och att man adderar konstanterna som finns framför? (Förlåt för dålig beskrivining, vet inte riktigt hur jag ska förklara:()
Helt rätt! Linjäriteten innebär alltså att man kan flytta ut summor och multiplikation med skalärer utanför operatorn.
Metod 2:
Ah okej! Men hur beräknar man då E(x^2)?
Du använder samma sats som tidigare, dvs Cov(X,Y)=E[XY]-E[X]E[Y], fast du använder du Y=X.
Kom ihåg att Cov(X,X)=Var(X)
Ah okej nu fick jag rätt svar med denna metod tack så mycket för hjälpen!


