beräkna asymptoter

Försöker lösa den här uppgiften. Vet att man ska sätta nämnaren till 0 för vertikala asymptoter, blir 0.5/-0.5. Hur gör man för de horisontella och sneda (vilken grad är nämnaren med absolutvärdet)?
För de horisontella asymptoterna: De uppkommer då x går mot någon oändlighet. Du kan dela upp beräkningen i "x går mot positiv oändlighet" och "x går mot negativ oändlighet". :)
Vad det gäller de sneda asymptoterna: Kan denna funktion ha en sned asymptot? Vilka andra asymptoter finns?
Tack,
När jag skriver in den i en graf ser jag att det inte blir några sneda. Man kanske kan visa det algebraiskt på nått sätt? (vet inte)
Hur många horisontella asymptoter har du? :)
2 tror jag
Dividera täljare och nämnare med x. Sedan kan du låta x gå mot oändligheten. Tänk på att undersöka alla olika fall.
unknown123 skrev:2 tror jag
Mycket riktigt! Det innebär att funktionen kommer att gå mot en horisontell linje för både positiva och negativa x (inte nödvändigtvis samma, dock). Då kan vi inte ha några sneda asymptoter. :)
tack för svaren
Om du är nöjd sätt gärna grönt.
varför kan den inte ha sneda asymptoter?
En funktion kan endast ha ett y-värde för varje x-värde. Eftersom vi har två horisontella asymptoter, kan vi skissa funktionen såhär:
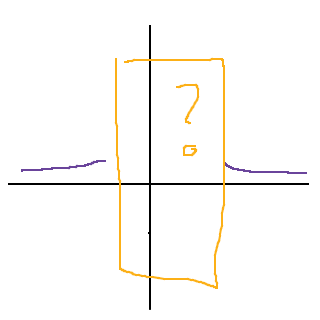
Det gulorangea området är ett mystiskt område (det är där vi är tillräckligt nära x = 0 för att funktionen ska bete sig lustigt), men när vi letar efter sneda och horisontella asymptoter bryr vi oss endast om vad som händer då x närmar sig olika oändligheter. Vi vet redan att om , då kommer vi att ha en horisontell asymptot, och om kommer vi också att ha en horisontell asymptot. Det finns helt enkelt ingen oändlighet kvar där vi skulle kunna ha en sned asymptot. :)
Om det finns vågräta asymptoter åt både höger och vänster, så finns det inte utrymme för några sneda asymptoter.



