Behöver jag skriva hur jag räknar ut n över k?
Hej, på prov behöver jag väl inte visa hur jag räknar ut någonting över nåt annat? De gör det ibland i boken och ibland inte. Jag har prov och läraren är borta så kan inte fråga henne.
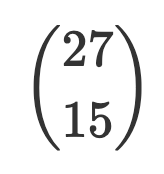
Du menar typ att bara skriva
"27 över 15" = 20058300
Jag hade nog tagit med mellanledet, det tar så lite tid att skriva ut.
Klart, är det ett prov med räknare och räknaren har denna funktion så behövs ingen närmare förklaring.
Skriver jag då bara 27 över 15 eller 27 nCr 15, om jag använder miniräknare?
Hejsan266 skrev:Skriver jag då bara 27 över 15 eller 27 nCr 15, om jag använder miniräknare?
Jag tror det beror på räknaren. Jag kan tyvärr inte dagens räknare och deras syntax. Eller menar du hur du skriver det i din lösning? Där använder du korrekt matematisk notation
Så här är det på min miniräknare:

I din lösning skriver du notation som Trinity2 har visat.
Tänkte i lösningen. Men mellantinget är inte ett måste att ha med, ellerhur?
MaKe skrev:Så här är det på min miniräknare:
I din lösning skriver du notation som Trinity2 har visat.
Min har nCr, stod även det i boken så trodde det var så för alla.
Är det en miniräknarfri del, så måste man skriva formeln och räkna:
(63)
Så jag antar att i en del där jag får använda miniräknaren måste jag inte skriva mellantinget?
Hejsan266 skrev:MaKe skrev:Så här är det på min miniräknare:
I din lösning skriver du notation som Trinity2 har visat.
Min har nCr, stod även det i boken så trodde det var så för alla.
Det verkar finnas flera olika beteckningar;
https://www.cuemath.com/ncr-formula/
men den absolut klassiska och mest korrekta är

hur den sedan anges vid beräkning beror på räknare/dator program. T.ex. är det i Mathematica
Binomial[27,15]
Hejsan266 skrev:Så jag antar att i en del där jag får använda miniräknaren måste jag inte skriva mellantinget?
Jag hade skrivit
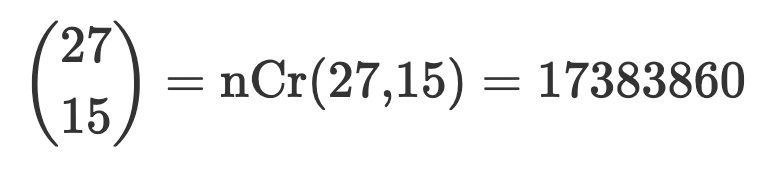
Då visar du
-- att du vet den klassiska notationen
-- hur du matar in på DIN räknare (om det nu skrives nCr... som exemplet visar, se även MaKe:s svar)
-- att du kan få fram rätt svar
Detta kan endast ge full pott vid rättning.
Sedan måste du motivera varför det är 27 över 15, och inte bara skriva "27 över 15".
Hejsan266 skrev:Så jag antar att i en del där jag får använda miniräknaren måste jag inte skriva mellantinget?
Nej, det hade varit orimligt att kräva att du skriver alla faktorer från 1 till 27 och sedan alla faktorer från 1 till 15. Det är för sånt vi har miniräknare.
Liten kommentar, jag vet inte vilka regler din lärare har, men jag tycker att ”27 över 15” är ett tydligare svar än 17383860 (eller ännu hellre 27 över 12). Liksom jag tycker att 22! ger mer information än 1124000727777607680000.
Det kan dock vara bra att känna till hur man snabbt beräknar ”n över k” för hand om man skulle behöva. Först skriver man ut k! i nämnaren. Därefter skriver man k st faktorer i täljaren, men nu räknar man nedåt med start vid n. Därefter förkortar man. Titta på bilden om du är intresserad.

(En litet intressant fundering är hur man kan veta att alla faktorerna i nämnaren försvinner vid förkortningen.)
!-notation är ett elegant format men ger ofta lite information om hur stort talet är. Det är svårt att relatera 15! till 27! Det är ungf. en faktor på 8 miljoner miljarder eller 8 * 10^15… 15! och 27! ger ingen "dimension" till detta. Det kan vara vara av värde att beräkna ett numeriskt resultat istället för en elegant matematisk "kort-form".
Trinity2 skrev:!-notation är ett elegant format men ger ofta lite information om hur stort talet är. Det är svårt att relatera 15! till 27! Det är ungf. en faktor på 8 miljoner miljarder eller 8 * 10^15… 15! och 27! ger ingen "dimension" till detta. Det kan vara vara av värde att beräkna ett numeriskt resultat istället för en elegant matematisk "kort-form".
Bra synpunkt, håller med! Att 22! ≈ 1,124 * 1021 kan man absolut behöva veta.
Och ser jag ”27 över 15” så har jag väldigt diffus uppfattning om att det är något i sjuttonmiljonersklassen vi talar om. Men kanske ska man inte bara trycka ”27 Konstig Symbol 15” på räknaren, utan först trycka in 27!, sen dela med 15! och därefter dela med 12! om man ska visa någon förståelse för begreppet.
Marilyn skrev:Trinity2 skrev:!-notation är ett elegant format men ger ofta lite information om hur stort talet är. Det är svårt att relatera 15! till 27! Det är ungf. en faktor på 8 miljoner miljarder eller 8 * 10^15… 15! och 27! ger ingen "dimension" till detta. Det kan vara vara av värde att beräkna ett numeriskt resultat istället för en elegant matematisk "kort-form".
Bra synpunkt, håller med! Att 22! ≈ 1,124 * 1021 kan man absolut behöva veta.
Och ser jag ”27 över 15” så har jag väldigt diffus uppfattning om att det är något i sjuttonmiljonersklassen vi talar om. Men kanske ska man inte bara trycka ”27 Konstig Symbol 15” på räknaren, utan först trycka in 27!, sen dela med 15! och därefter dela med 12! om man ska visa någon förståelse för begreppet.
På min tid gav räknarna upp efter 10^99, sedan ökade det till 10^499 (vissa HP-modeller). Idag kan de nog via appar ge godtycklig stora och exakta svar givet man håller sig inom datorns/CPU:s talområde. Det är imponerande vad Mathematica och Maple kan spotta ur sig från de mest simpla kommando och uttryck. Jag minns en "trivial" integral som Gert Almkvist, Lund, en gång visade och dess svar i Maple, som var monstruöst stort. Den primitiva funktionen var säker 30 sidor lång, och integranden var "oansenlig". Tyvärr kommer jag ej ihåg integralen.
Haha, spännande! I sådana lägen är man ganska pantad utan assistans. Men det man brottas med i klassrummet är ofta mer blygsamma uppgifter. Häromdagen hjälpte jag en gymnasieelev som rutinmässigt sträckte sig efter räknaren för att beräkna 0,1 / 0,1.
Häromdagen hjälpte jag en gymnasieelev som rutinmässigt sträckte sig efter räknaren för att beräkna 0,1 / 0,1.
Jag är mer skyldig till det här brottet än vad jag vill medge. Jobbar ändå en del matematik men aritmetiken alltså... Det är hopplöst. Senaste tentan slog jag konstant saker som 14+8 och 3-4 på räknaren bara för att bekräfta att matematiken inte uppdaterats sedan jag sist räknade.
Har mer än ett antal gånger missat poäng för att jag gjort dumma aritmetikfel. Det är helt omöjligt att åtgärda.
naytte skrev:Häromdagen hjälpte jag en gymnasieelev som rutinmässigt sträckte sig efter räknaren för att beräkna 0,1 / 0,1.
Jag är mer skyldig till det här brottet än vad jag vill medge. Jobbar ändå en del matematik men aritmetiken alltså... Det är hopplöst. Senaste tentan slog jag konstant saker som 14+8 och 3-4 på räknaren bara för att bekräfta att matematiken inte uppdaterats sedan jag sist räknade.
Har mer än ett antal gånger missat poäng för att jag gjort dumma aritmetikfel. Det är helt omöjligt att åtgärda.
Ha! Et tu, Naytte! Du är inte ensam! Då matematik är en "vetenskap i rörelse" gäller det att vara påpasslig! Skämt åsido, det finns falanger sedan många år (ofta utsända Mathematica/Maple-evangelister) som vill reformera matematikundervisningen från "beräkning" till "modellering". Det är en intressant aspekt. Jag har inte bildat mig någon fast uppfattning i frågan. Jag ser poänger i båda läger. Vi står i ett teknologiskt vägskäl mer än någonsin idag… Jag har ingen universell lösning. Vad hade Gauss och Euler gjort om de haft Mathematica/Maple?
Jag har absolut blivit sämre på huvudräkning sedan räknarna kom. Men det är en sak, det trista tycker jag är när elever slår in ”gånger 3” på räknaren och i nästa andetag (eller samma) slår in ”delat med 3”. Oavsett beräkning eller modellering så tror jag på att man gör förenklingar innan man lämnar över till tekniken.
Ha! Et tu, Naytte!
Jo då, riktigt ordentligt.
Mina lärare på låg- och mellanstadiet trodde att jag hade inlärningssvårigheter eller någon nedsättning eftersom jag inte tycktes kunna lära mig gångertabellerna. Egentligen handlade det inte om dumhet, utan 9-åriga jag var bara hardcore Maple-evangelist... 😉
Vad hade Gauss och Euler gjort om de haft Mathematica/Maple?
Jag har faktiskt ställt mig själv exakt samma fråga tidigare! Svårt att svara på dock. Jag håller nog med dig egentligen, det finns bra argument i båda läger.
Marilyn skrev:Jag har absolut blivit sämre på huvudräkning sedan räknarna kom. Men det är en sak, det trista tycker jag är när elever slår in ”gånger 3” på räknaren och i nästa andetag (eller samma) slår in ”delat med 3”. Oavsett beräkning eller modellering så tror jag på att man gör förenklingar innan man lämnar över till tekniken.
Ja, det är här jag är kluven. De ligger ofta en poäng i "komplexa uttryck" jämfört med förenklade då de komplexa, även om de innehåller trivial förenklingar, kan beskriva en progression, t.ex. i en talföljd. Genom att förenkla i varje steg döljer man ev. den generella formen. Själv är jag allergisk mot 1.5 när det finns fina tal som 3/2 och det kryper i kroppen på mig när jag ser kapitel om närmevärden och signifikanta siffror. Matematik är _exakt_ :)
Föga anade Hejsan266 att denna tråd skulle bli den geometriska orten för personliga bekännelser. Det blir stället vi uppsöker för bikt och försoning. Hit kan framtida generationer vallfärda och förundras – även S:t Trinity2 hade stunder av svaghet, och S:t naytte slog en gång 14+8 på räknaren! Det är bra om folk förstår att också mattelärare kan anfäktas av tvivel.
”Själv är jag allergisk mot 1.5 när det finns fina tal som 3/2 ”; visst håller vi med – men verkligheten är komplex även för en matematiklärare. Många av de modeller vi hanterar har sitt ursprung i världen. Om inte universum hade haft några rumsdimensioner så skulle Euklides kanske aldrig ha funderat över trianglar och Pythagoras aldrig ha formulerat sin sats. Även om vi ser på verkligheten med misstro, så kan vi inte helt räkna bort den som inspiratör till den obefläckade matematiken.
Jag sitter på höjden h över vattenytan och ser ut över ett spegelblankt hav med avståndet d till horisontlinjen.
Då är d2 proportionellt mot h.
Inte exakt, på ett perfekt klot blir det exakta avståndet en Taylorutveckling. Ifall höjden är liten jämfört med jorddiametern så kan man för praktiskt bruk knipsa av svansen.
Det handlar alltså inte om att vi approximerar en knagglig jordyta med en exakt sfär, det är det ideala objektet som vi approximerar med första termen i en oändlig serie.
Det tycker jag är matematik.
Men i mycket tänker vi säkert lika. En rätvinklig triangel avbildas i boken. Det finns ingen angiven koppling till verkligheten, hypotenusan är 2 och en katet 1, vad är den andra kateten? Här blir svaret 1,7 larvigt, man borde såklart svara med roten ur 3, ingen bryr sig om närmevärdet. Fast ska vi beräkna motsvarande sträcka på en triangelformad tomt med katet 100 och hypotenusa 200 meter; då kan svaret sqr 30000 meter kännas ofullständigt.
Vi möter problem i verkligheten, för att angripa dem skapar vi modeller som vi kan räkna på. I modellerna har vi tagit bort allt som är ”verkligt”, linjer är räta och det finns inget luftmotstånd. När modellen skänkt oss ett resultat behöver vi anpassa detta till ursprungsproblemet. I det läget behöver inte ett närmevärde vara skämmigt.
”Genom att förenkla i varje steg döljer man ev. den generella formen.”
Kanske det, har inte sett det så. Ett värre problem tror jag är att man fått ett krångligt trigonometriskt uttryck. I stället för att förenkla sätter man in vinkeln v = 30° och får 0,57735. Man missade att uttrycket kunde förenklas till tan v.
S:t M
Så länge vi inte möter div. helgons historiska öden.
Tack för hjälpen iallafall.




