Behöver hjälp med en redovisningsuppgift - Fiskodling
Den som odlar fisk i en damm vill naturligtvis ta upp fisken när den sammanlagda vikten är maximal. För en viss laxfisk gäller:
1.
Fiskens längd l cm ges av formeln
Där t månader är den tid fisken varit i dammen.
2. fiskens vikt i gram ges av tabellen:
Längd/cm 10.1 25.0 32.0 35.4 43.8 45.5 55.7
..........vikt/g 15 236 520 660 1250 1425 2590
3. Fiskens livslängd kan bestämmas ur formeln:
Där n är antalet fiskar av 1000 utplanterade som finns kvar t månader efter utplanteringen.
Hur länge bör fisken vara kvar i dammen?
- - - - -
Har försökt lösa ut den på olika sätt och både tagit längden(istället för vikt) * livslängden och därefter tagit den funktionens derivata = 0, därefter fått ut svaret t=17 månader, dock har jag sökt lite på internet och sett både 17 månader och 34 månader som svar, samtidigt har jag sett att t=17 är fel (?). Har försökt nu att ta där m är vikten och där c är enligt tabellen 0,015kg och därefter multiplicerat det med N, sedan har jag försökt derivera det men det blir väldigt omständigt att derivera (väldigt lång derivering), dock blir maxpunkten enligt räknaren t=34 för funktionen. Vet inte riktigt om det är rätt metod? Hur ska jag göra/fortsätta?
Det finns lite olika sätt att lösa uppgiften, men i grund och botten vill du göra följande:
Bestäm totala vikten som funktion av tiden, V(t)
Hitta maximum för V(t)
Det du har är längden per fisk som funktion av tiden (l(t)), antalet fiskar som funktion av tiden (N(t)) och vikten som funktion av längden (värdetabell). Du har rätt i att V(t)=N(t)m(t)=n(t)m(l(t)), och m=cl^3 är en bra ansats. Om du använder räknarens kurvanpassningsverktyg ser du att du kommer väldigt nära de uppmärkta värdena.
Sen är det helt rätt att du vill derivera, men lyckas du inte med deriveringen så har du gjort helt rätt som letar maximum grafiskt.
Är det dåligt att säga att man ba slog in det på räknaren. Känns som att det är bättre om man deriverar själv....
Jag tycker att du ska derivera själv, för så himla svår derivata är det inte. Däremot kommer du få problem att hitta nollställena till derivatan analytiskt, så riktigt hela vägen kommer du ändå inte.
har försökt derivera redan, alltså derivera denna funktionen:
har haft stora problem att derivera denna, förstår att jag förmodligen måste använda mig av produktregeln men antagligen har jag gjort fel någonstans. Hur ska jag börja derivera? Har börjat multiplicera in 80 med 1-0.96^t, är det fel?
Ja, det är att göra det onödigt komplicerat för sig. Bryt ut 0.015*80^3*1000 som en konstant - den behöver du inte bry dig om när du deriverar. Kvar har du som du deriverar med produktregeln (och så multiplicerar du med konstanen i slutet (eller låter bli, eftersom du ändå bara är intresserad av eventuella nollställen)).
Detta är min derivering, det verkar väl stämma? Hur går man vidare sedan för att kunna räkna ut t?
Ah, jag slarvade när jag deriverade innan, det här kan du visst lösa analytiskt.
Din derivering stämmer helt. Du är ju intresserad av när derivatan är noll. En av dina faktorer måste alltså vara noll, och jag tror att du ganska lätt kan se vilken av dem (tre av dem är aldrig 0 för t>0). Sätter du den faktorn = 0 så får du en ekvation som du klarar av att lösa (med matte 2-kunskaper, om jag minns rätt på vad som kommer i vilken kurs).
Det var lättare att derivera än jag trodde, krånglade till det med att inte bryta ut det som inte var relevant.Tack så hemskt mycket för hjälpen!
hej! undrar bara vart, 0,015 kom ifrån? samt varför blev det (80(1−0.96t))^3
varför gör man upphöjt med 3
hej nu kommer jag här lite senare men jag förstår inte heller vad 0,015 kommer ifrån
Gammal tråd, men försök till svar.
Tabellen i uppgiften ger fiskens massa givet längd.
Om du anpassar en potensfunktion till dessa data så ser den ut så här:
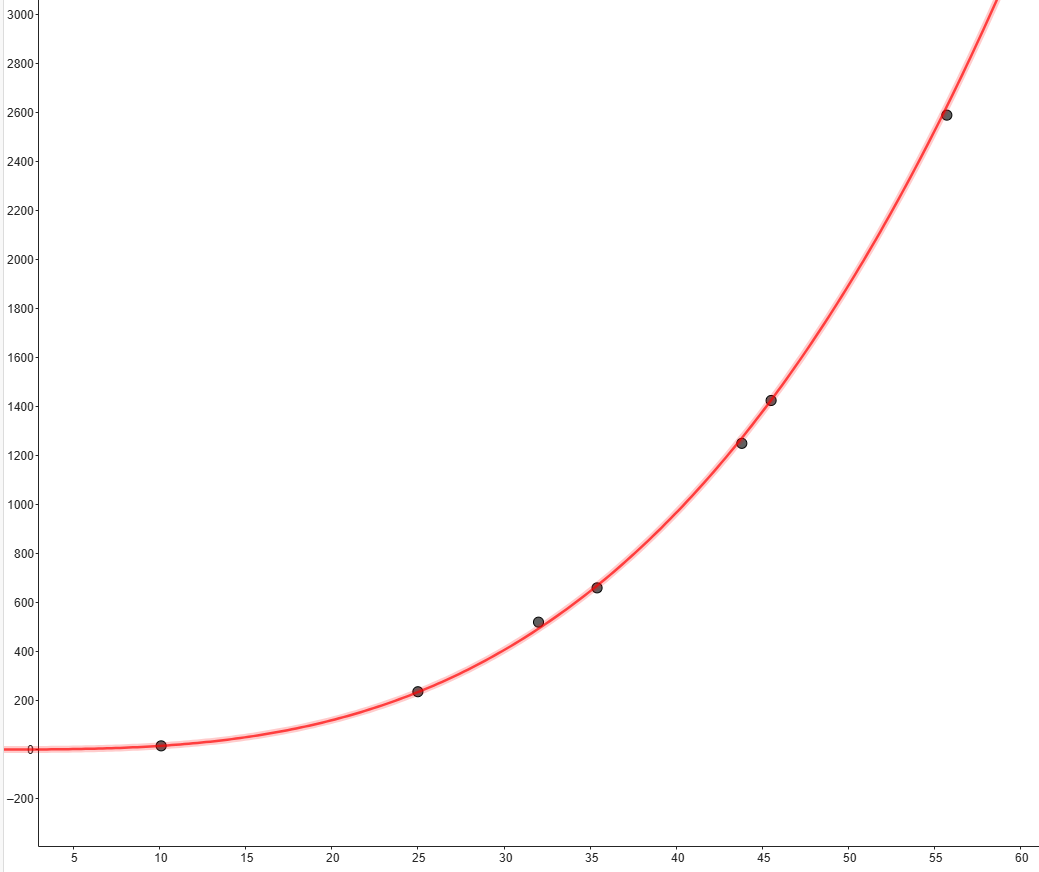
Det är fiskens massa som en funktion av längden.
Där har du ditt 0,015 (som borde vara ett 0,0142). Å andra sidan spelar det ingen roll för uppgiften.
Nu är det ju tid vi är intresserade av och vi har även en funktion för längd över tid:
Så in med den i vår potensfunktion för massan, som då istället blir en funktion över tid:
Sedan för att få totala massan fisk kan vi multiplicera med antalet fiskar över tid (givet i uppgiften).
Då får vi något som ser ut så här:

Derivatan (röd) har ett nollställe vid t≈34 månader. Då har vi ≈820 kg fisk i dammen.

