Begynnelsevärdeproblem
Stressad och trött inför tenta imorgon är det frustrerande att inte kunna lösa detta, snälla hjälp mig!
Försöker såhär:
Men enligt facit
yh uppfyller väl inte y(0) = 0 och y'(0) = 0.
Måste väl vara fel i facit?
Hmm, tar tillbaka detta. I problemet ges y(0) och y'(0). Inte yh.
Skall kolla.
Hmm, enligt matteboken skall detta gälla:
Om r1=s+itr1=s+it och r2=s−itr2=s−it så kan lösningarna skrivas på formeln:
y=e^sx(C1costx+C2sintx)
Det är fel i facit.
Härifrån ges:
yh=c1*sin(x) + c2*cos(x)
Dracaena,
gulgubben har ju bara räknat ut yh(dock med fel ansats), du har ju räknat ut yh+yp.
Enligt vad jag förstår.
ydracena(0) = 0
y'dracena(0)=0
Dracaena skrev:Det är fel i facit.
Yes, detta är lösningen i facit, har fått yp till 1/2 e^x, men homogenlösningen får jag inte fram, alltså cos o sin.
y=yp+yh
Jaha, jag missade att facit bara var , my bad.
Analys skrev:Dracaena,
gulgubben har ju bara räknat ut yh(dock med fel ansats), du har ju räknat ut yh+yp.
Enligt vad jag förstår.
ydracena(0) = 0y'dracena(0)=0
sorry att jag rört till det, men jag lyckas alltså inte lösa ut yh, enligt ovan. yp är jag med på!
Detta är fel ansats:
Acos(−x)+Bsin(x)
Skall vara + inom båda trigfunktionerna.
Det spelar ingen roll att det står cos(-x) eftersom cos(x) är jämn.
Du kan inte stoppa in dina Begynnelsevärden i yh, det gäller ju för y(x)!
Du måste först hitta och sedan kan du ta reda på och .
Dracaena skrev:Det spelar ingen roll att det står cos(-x) eftersom cos(x) är jämn.
Du kan inte stoppa in dina Begynnelsevärden i yh, det gäller ju för y(x)!
Du måste först hitta och sedan kan du ta reda på och .
Tusen tack!!!
Av lathet så räknade jag den i Mathematica, men om du fastnar så säg till. 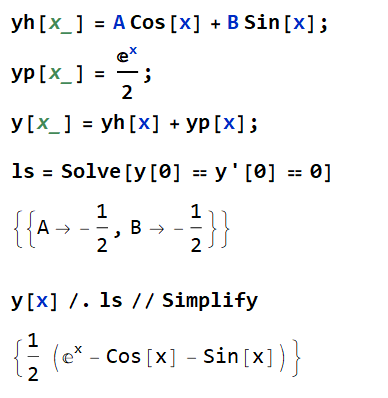
I värsta fall så ser du vilka steg du skall ta för att lösa uppgiften.



