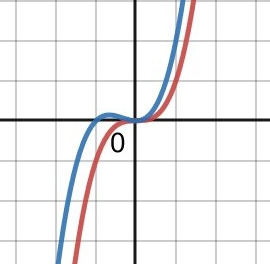
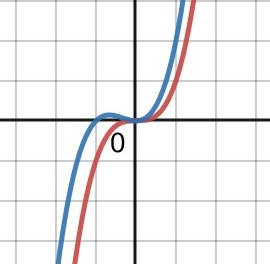
begrepp inom derivata
extrempunkter
lokala/globala maximi/minimi punkter --> finns det en tumregel för hur man avgör dessa?
terasspunkt
Känns som jag rör ihop dessa begrepp och har inte riktigt fått en klar uppfattning om vad varje är..
En funktion kan ju ha flera maximi- och minimipunkter. Dessa är lokala. Globala max- och minpunkter är de största respektive minsta värdena som funktionen någonsin antar.
En terasspunkt är en punkt där och grafen är växande eller avtagande på båda sidor av punkten.
naytte skrev:En funktion kan ju ha flera maximi- och minimipunkter. Dessa är lokala. Globala max- och minpunkter är de största respektive minsta värdena som funktionen någonsin antar.
En terasspunkt är en punkt där och grafen är växande eller avtagande på båda sidor av punkten.
globala max och minipunkter kan väl vara vart som helst i grafen så länge de har de största/minsta värdena i funktionen?
och en terasspunkt är egentligen mittpunkten i en "dal"? i grafen då? (en terasspunkt har alltid derivatan 0 då?)
en extrempunkt? är det bara alla lokala punkter?
globala max och minipunkter kan väl vara vart som helst i grafen så länge de har de största/minsta värdena i funktionen?
Globalt maximum = det högsta y-värdet av alla, och motsvarande för globalt minimum.
och en terasspunkt är egentligen mittpunkten i en "dal"? i grafen då? (en terasspunkt har alltid derivatan 0 då?)
Den röda kurvan har en terrasspunkt (derivatan är +0+). Den blå kurvan har ett lokalt maximum (derivatan är +0-) och ett lokalt minimum (derivatan är -0+).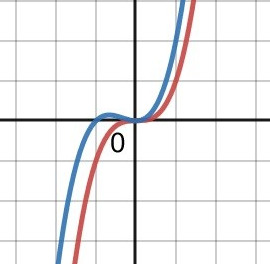
en extrempunkt? är det bara alla lokala punkter?
Extrempunkter är ett samlingsnamn för maximipunkter och minimipunkter.
Smaragdalena skrev:globala max och minipunkter kan väl vara vart som helst i grafen så länge de har de största/minsta värdena i funktionen?
Globalt maximum = det högsta y-värdet av alla, och motsvarande för globalt minimum.
och en terasspunkt är egentligen mittpunkten i en "dal"? i grafen då? (en terasspunkt har alltid derivatan 0 då?)
Den röda kurvan har en terrasspunkt (derivatan är +0+). Den blå kurvan har ett lokalt maximum (derivatan är +0-) och ett lokalt minimum (derivatan är -0+).
en extrempunkt? är det bara alla lokala punkter?
Extrempunkter är ett samlingsnamn för maximipunkter och minimipunkter.
tack för klargörandet!
men det är skillnad på globala och lokala maximivärden/punkter väl?
värden -> då är man ute efter högsta y-värdet i funktionen?
punkt --> en koordinat?
naturnatur1 skrev:Smaragdalena skrev:globala max och minipunkter kan väl vara vart som helst i grafen så länge de har de största/minsta värdena i funktionen?
Globalt maximum = det högsta y-värdet av alla, och motsvarande för globalt minimum.
och en terasspunkt är egentligen mittpunkten i en "dal"? i grafen då? (en terasspunkt har alltid derivatan 0 då?)
Den röda kurvan har en terrasspunkt (derivatan är +0+). Den blå kurvan har ett lokalt maximum (derivatan är +0-) och ett lokalt minimum (derivatan är -0+).
en extrempunkt? är det bara alla lokala punkter?
Extrempunkter är ett samlingsnamn för maximipunkter och minimipunkter.
tack för klargörandet!
men det är skillnad på globala och lokala maximivärden/punkter väl?
värden -> då är man ute efter högsta y-värdet i funktionen?
punkt --> en koordinat?
Den röda kurvan har ingen maximi- eller minimipunkt, kurvan kan ju fortsätta uppåt och neråt hur långt som helst.
Den blå kurvan har ett lokalt maximum och ett lokalt minimum, men inga globala extrempunkter - den kan ju fortsätta uppåt och neråt hur långt som helst.
Smaragdalena skrev:Den röda kurvan har ingen maximi- eller minimipunkt, kurvan kan ju fortsätta uppåt och neråt hur långt som helst.
Den blå kurvan har ett lokalt maximum och ett lokalt minimum, men inga globala extrempunkter - den kan ju fortsätta uppåt och neråt hur långt som helst.
den röda har väl en lokal minipunkt?
vad är skillnaden mellan att "hitta ett lokalt mini/maxivärde"
och att "hitta en lokal mini/maxipunkt" ?
den röda har väl en lokal minipunkt?
Var skulle den vara, menar du?
vad är skillnaden mellan att "hitta ett lokalt mini/maxivärde"
och att "hitta en lokal mini/maxipunkt" ?
I det första fallet handlar det bara om y-värdet, i det andra fallet om koordinaterna (x,y).
Smaragdalena skrev:den röda har väl en lokal minipunkt?
Var skulle den vara, menar du?
vad är skillnaden mellan att "hitta ett lokalt mini/maxivärde"
och att "hitta en lokal mini/maxipunkt" ?
I det första fallet handlar det bara om y-värdet, i det andra fallet om koordinaterna (x,y).
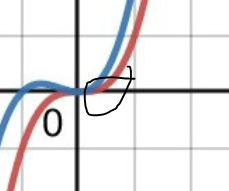där, eller nu inser jag att lutningen kanske inte helt är 0?
eller hur resonerar man?
Derivatan av f(x) = x3 är f'(x) = 3x2. När x = 0 är även derivatan lika med 0, men det är en terrasspunkt, ingen minimipukt.
Smaragdalena skrev:Derivatan av f(x) = x3 är f'(x) = 3x2. När x = 0 är även derivatan lika med 0, men det är en terrasspunkt, ingen minimipukt.
då är jag med, tack snälla
