Befolkningstätheten av en stad, hitta antalet invånare som bor mellan 1 km och 4 km.

shkan skrev:

Hej!

Uppgiften lyder så här:

"I en stad kan antalet invånare per kvadratkilometer beräknas enligt sambandet: $\frac{10000}{x\sqrt{x}}$, där x är avståndet till stadens centrum. Hur många personer bor på avstånd mellan 1 km och 4 km?"

---

Först tänkte jag att lösa problemet genom att säga att g(x) beskriver antalet invånare.

 

g''(x) = $\frac{10 000}{x\sqrt{x}}$

 

sedan tänkte jag att hitta den generella integralen till g''(x), dvs g'(x): $\int \frac{10 000}{x\sqrt{x}}$dx.

Men då hittade jag ett problem i lösningen: när jag tar integralen så får jag en konstant som jag kan inte på något sätt ta bort eller ersätta ett värde med, så lösningsmetoden blir felaktigt. Jag ville därefter ta integral från 1 till 4 av g'(x), men som sagt så skulle det inte leda någonstans.

---

Jag försökte sedan hitta gamla trådar som kanske har löst den här problemet. Jag lyckades hitta en, men tråden blev lite komplicerad för mig. Som jag förstår måste man integrera:

 

${\int }_1^4\frac{10 000}{x\sqrt{x}}2\mathrm{\pi x} \mathrm{dx}$

 

Jag undrar bara hur man kom fram till denna integral för att det är ganska svårt för mig att hitta den. 

Som vanligt: Börja med att rita!

Först kan vi titta på funktionen $f\left(x\right)\hspace{0.17em}=\frac{10 000}{x\sqrt{x}}$. Den ser ut så här: 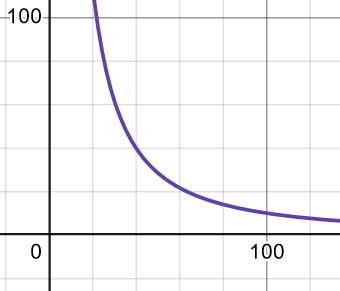Vad är det funktinen visar? Hur många personer det bor per kvadratkilometer på ett visst avstånd från stadens centrum. Om man är 1 km från centrum är befolkningstätheten 10 000 inv/km2, 4 km från centrum har den sjunkit till 1 250. (Precis i centrum skulle befolkningstätheten vara oändlig men det behöver vi inte räkna på). Om befolkningstätheten hade varit konstant skulle vi ha räknat ut arean av en cirkelring med ytterradie 4 km och innerradie 1 km och multiplicerat med (den konstanta) befolkningstätheten, men eftersom befolkningstätheten varierar behöver vi använda en integral istället. Det är från denna cirkelring man får faktorn $2\mathrm{\pi x}$, där x är avståndet från centrum.

Smaragdalena skrev:

shkan skrev:

Hej!

Uppgiften lyder så här:

"I en stad kan antalet invånare per kvadratkilometer beräknas enligt sambandet: $\frac{10000}{x\sqrt{x}}$, där x är avståndet till stadens centrum. Hur många personer bor på avstånd mellan 1 km och 4 km?"

---

Först tänkte jag att lösa problemet genom att säga att g(x) beskriver antalet invånare.

 

g''(x) = $\frac{10 000}{x\sqrt{x}}$

 

sedan tänkte jag att hitta den generella integralen till g''(x), dvs g'(x): $\int \frac{10 000}{x\sqrt{x}}$dx.

Men då hittade jag ett problem i lösningen: när jag tar integralen så får jag en konstant som jag kan inte på något sätt ta bort eller ersätta ett värde med, så lösningsmetoden blir felaktigt. Jag ville därefter ta integral från 1 till 4 av g'(x), men som sagt så skulle det inte leda någonstans.

---

Jag försökte sedan hitta gamla trådar som kanske har löst den här problemet. Jag lyckades hitta en, men tråden blev lite komplicerad för mig. Som jag förstår måste man integrera:

 

${\int }_1^4\frac{10 000}{x\sqrt{x}}2\mathrm{\pi x} \mathrm{dx}$

 

Jag undrar bara hur man kom fram till denna integral för att det är ganska svårt för mig att hitta den. 

Som vanligt: Börja med att rita!

Först kan vi titta på funktionen $f\left(x\right)\hspace{0.17em}=\frac{10 000}{x\sqrt{x}}$. Den ser ut så här: Vad är det funktinen visar? Hur många personer det bor per kvadratkilometer på ett visst avstånd från stadens centrum. Om man är 1 km från centrum är befolkningstätheten 10 000 inv/km2, 4 km från centrum har den sjunkit till 1 250. (Precis i centrum skulle befolkningstätheten vara oändlig men det behöver vi inte räkna på). Om befolkningstätheten hade varit konstant skulle vi ha räknat ut arean av en cirkelring med ytterradie 4 km och innerradie 1 km och multiplicerat med (den konstanta) befolkningstätheten, men eftersom befolkningstätheten varierar behöver vi använda en integral istället. Det är från denna cirkelring man får faktorn $2\mathrm{\pi x}$, där x är avståndet från centrum.

Hej Smaragdalena! Jag undrade bara om du har andra lösningsvägar som du kan visa mig för att jag förstår inte hela idén med att skapa en cirkel med ytterradie 4 och innerradie 1. Finns det andra sätt att lösa uppgiften? Tack så mycket.

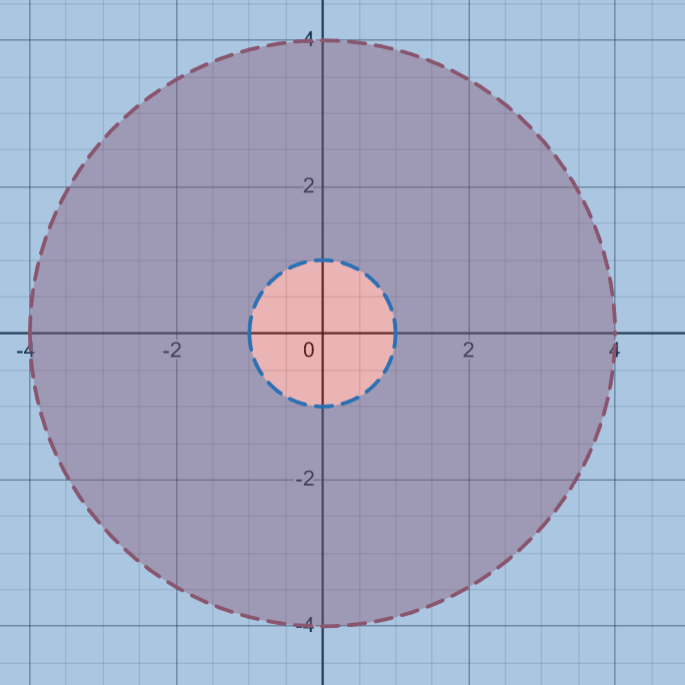
Är du med på att man vill räkna ut hur många invånare det finns i den mörka cirkelringen, d v s de som bor längre bort från centrum än 1 km men närmare än 4 km?

Smaragdalena skrev:

Är du med på att man vill räkna ut hur många invånare det finns i den mörka cirkelringen, d v s de som bor längre bort från centrum än 1 km men närmare än 4 km?

Hej Smaragdalena. Jag ville bara säga att jag förstår konceptet nu. Jag lyckades förstå för ungefär 2 timmar sedan. Tack för ditt hjälp! Vad jag förstår är att, när man tar integralen från 1 till 4 av funktionen * 2pi*x, så hittar man arean som personerna mellan 1 och 4 km bor (2pi*x), och sedan multiplicerar man med befolkningstätheten så får man invånare mellan 1 och 4 km. Kanske min förklaring eller förståelse är lite fel, jag vet inte.

Egentligen tror jag det är nog så här:

Låt oss säga att x är 1. Arean av området där personerna bor 1 km från centrum kan beräknas med 2*pi*dx. Sedan multiplicerar man befolkningstätheten i det där området, i det här fallet 10000 inv/km^2. Då får man svaret 20000*pi*dx invånare. Man fortsätter göra den här algoritmen tills man når fram x = 4, och då slutar man algoritmen. Sedan adderar man ihop alla dessa invånare ihop, och man får ungefär 126000 inv.

Vad jag förklarade ovanför är bara intutionen bakom integralen från 1 till 4 av xf(x)*2pi*dx. Svaret blir ungefär 126 000 personer (invånare).

Snälla säg till om min intution är fel, jag vill förstå alla problem som jag utför så att jag faktiskt förstår och kan applicera den nya kunskapen till andra problem. 

Tack så mycket! 

Det verkar som om din intuition är riktig. Stämmer ditt svar med facit?

Smaragdalena skrev:

Det verkar som om din intuition är riktig. Stämmer ditt svar med facit?

Ja! Det stämmer riktigt. Tack!