Bäring polära koordinater

Hej, har en uppgift där man ska bestämma bäringen från Göteborg till Mekka. Alltså vinkeln relativt nordriktningen i horisontalplanet i Göteborg, givet vinklarna $θ, ϕ$ i polära koordinater för de två platserna.

Jag tänkte att det gick att lösa uppgiften genom att bilda vektorerna G och M från jordens mitt till Göteborg respektive jordens mitt till Mekka och N från jordens mittpunkt till nordpolen. Sedan se att G och N spänner upp ett plan genom Göteborg och nordpolen och att G och M spänner upp ett plan genom Göteborg, jordens centrum och Mekka. $G = (\begin{matrix} \sin (θ) \cos (ϕ) \\ \sin (θ) \sin (ϕ) \\ \cos (θ) \end{matrix})$ , $N = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}), M = (\begin{matrix} \sin (θ') \cos (ϕ') \\ \sin (θ') \sin (ϕ') \\ \cos (θ') \end{matrix})$ .

Sedan tar jag kryssprodukten mellan G och N resp mellan G och M för att få normalvektorer till de två planen, sedan tänker jag att den sökta vinkeln är vinkeln mellan dessa normalvektorer. Men något blir fel. Har suttit med uppgiften vid ett antal olika tillfällen och testat olika metoder men kommer inte framåt längre.

Tacksam för hjälp.

(Raderat. Tänkte fel. )

Kanske lättare att ta fram tangentvektorer till cirkelbågarna mellan vektorerna och räkna ut vinkel mellan dessa. $\vec{T}$ pekar mot norr, $\vec{τ}$ mot Mecka.

PATENTERAMERA skrev:
Kanske lättare att ta fram tangentvektorer till cirkelbågarna mellan vektorerna och räkna ut vinkel mellan dessa. $\vec{T}$ pekar mot norr, $\vec{τ}$ mot Mecka.

Det var smart med trippelprodukt, jag antar att längden av ditt tau och T blir 1 eftersom vektorerna kan väljas till den längden utan att påverka vinklarna. Jag fick fram uttrycket: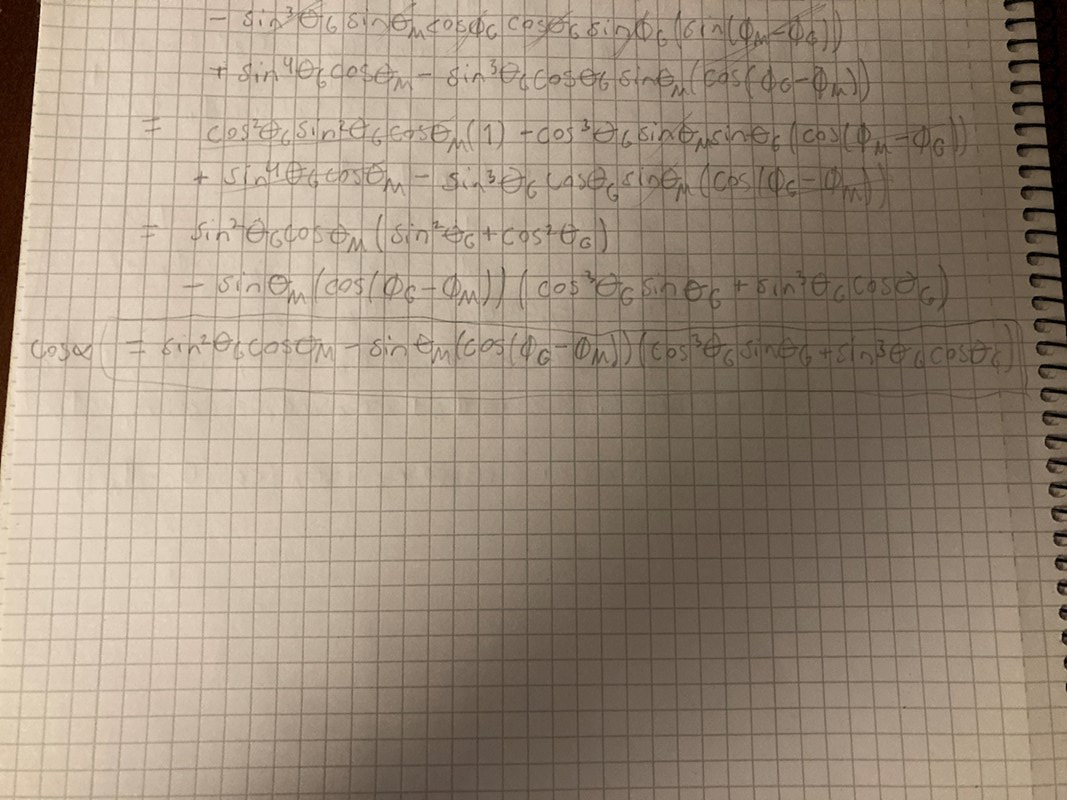

Som dock inte heller ger mig rätt vinkel alpha, suck. Metoden känns ju väldigt rimlig och jag förstår inte varför det blir fel har du räknat och fått något annat svar/ser något fel i mitt? Tack för hjälpen.

Nej, har inte gjort beräkningarna. Men man kan inte utgå från att det blir enhetsvektorer.

PATENTERAMERA skrev:
Nej, har inte gjort beräkningarna. Men man kan inte utgå från att det blir enhetsvektorer.

Okej. Jag satte in uttrycket (med längderna också) i Matlab men det ger mig felaktiga svaret 110 grader. Blev väldigt jobbiga uttryck att räkna med i alla olika metoder jag testat, men här är koden där översta raden är det inringade uttrycket från pappret ovan och resterande är kvoten av längderna för tau och T som jag inte "orkade" förenkla mer om det ändå inte stämmer :/, tg, pg osv står allså för theta_g och phi_g...

v=(sin(tg))^2*cos(tm)-(sin(tm)*cos(pg-pm))*((cos(tg))^3*sin(tg)+(sin(tg))^3*cos(tg))... /((sin(tg)*cos(tg)*cos(tg))^2+(cos(tg)*sin(tg)*sin(tg))^2+(sin(tg))^4)^0.5...*(((sin(tg)^2)*sin(tg)*sin(tm)*(sin(pm-pg))-((cos(tg))^2*sin(tm)*cos(pm))...+cos(tg)*cos(tm)*sin(tg)*cos(pg))^2+((cos(tg)*cos(tm)*sin(tg)*sin(pg)...-(cos(tg))^2)*sin(tm)*sin(pm)-(sin(tg)^2)*sin(tm)*cos(pg)*(sin(pm-pg)))^2 ...+(-cos(tm)*(sin(tg))^2+sin(tg)*cos(tg)*sin(tm)*cos(pg-pm))^2)^0.5

Där v= $\cos (α)$ .

Hitta eventuella fel här känns som att leta efter en nål i en höstack. Har vi gjort ett teoretiskt fel eller ett beräkningsfel?

Om man googlar så hittar man:

Tydligen så är vinkeln mellan normalerna som du räknade ut $π - α$ så du kan ju börja med att se om pi minus ditt första värde på vinkeln mellan normalerna ger rätt. Eller du får kanske räkna i grader.

Annars vore det bra om du kunde redovisa hela uppgiften så att vi kan titta exakt på vilka siffror som ges.

PATENTERAMERA skrev:
Hitta eventuella fel här känns som att leta efter en nål i en höstack. Har vi gjort ett teoretiskt fel eller ett beräkningsfel?

Om man googlar så hittar man:

Tydligen så är vinkeln mellan normalerna som du räknade ut $π - α$ så du kan ju börja med att se om pi minus ditt första värde på vinkeln mellan normalerna ger rätt. Eller du får kanske räkna i grader.

Annars vore det bra om du kunde redovisa hela uppgiften så att vi kan titta exakt på vilka siffror som ges.

Japp insåg att min första ide' stämde när jag testade att måla upp i geogbra med givna värdena, nu återstår bara att göra en lösning för hand med de jobbiga uttrycken som faktiskt stämmer, tack för hjälpen.

Ett litet problem här är ju att vi bara får vinkeln mot norr, men inte någon indikation om det är en avvikelse mot öster eller väster. Men man kanske vet att Mecka ligger åt öster. Eller så får man analysera djupare.

Svara

Visa senaste svar