Balk

Snitta och frilägg balken.

Ansätt en momentekvation kring en av bockarna.

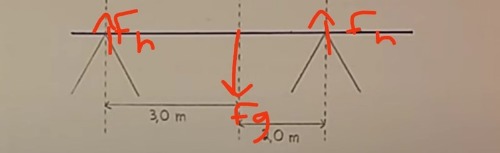
Vet inte om du är ute efter det här?

Momentekvationen... Hur blir det här? Jag vet att f1 × r1 = f2 × r2

Men här har vi endast vikten på balken och avstånden. 

Vi vill få fram f1 och f2, så egentligen ska man väl kasta om i formeln men vi har 2 okända?

I din bild har du kallat båda krafterna $F_h$. Krafterna från bockarna behöver inte vara lika stora. Kalla dem olika saker t.ex. $F_a$ och $F_b$.

Du har också märkt ut en tyngdkraft $F_g$

Vad ska gälla för krafterna? (Kraftjämvikt).

Välj en av bockarna som momentpunkt. Det spelar ingen roll vilken du väljer, men du måste välja en punkt.

Hur lång hävarm får $F_g$ till din valda punkt? Hur lång hävarm får kraften från bocken på andra sidan?

D4NIEL skrev:

I din bild har du kallat båda krafterna $F_h$. Krafterna från backarna behöver inte vara lika stora. Kalla dem olika saker t.ex. $F_a$ och $F_b$.

Lite slarvigt av mig! Skulle stå Fn (som normalkraft) (: men jag kallar de för f_a och f_b nu. (Hur vet vi att de inte är lika stora? Är det för att det är olika avstånd till tyngdpunkten?)

Du har också märkt ut en tyngdkraft $F_g$

Vad ska gälla för krafterna? (Kraftjämvikt).

 

Välj en av bockarna som momentpunkt. Det spelar ingen roll vilken du väljer, men du måste välja en punkt.

Med momentpunkt, är det alltså en punkt där en kraft finns, eller är det valfritt område? Vart är enklast att lägga den punkten? 

Hur lång hävarm får $F_g$ till din valda punkt?Hur lång hävarm får kraften från backen på andra sidan?

Det här förstår jag inte riktigt. (har inte läst fysik 2 än).

Men vi säger jag väljer punkten Fa (är vänster), så 3m.

naturnatur1 skrev:

Lite slarvigt av mig! Skulle stå Fn (som normalkraft) (: men jag kallar de för f_a och f_b nu. (Hur vet vi att de inte är lika stora? Är det för att det är olika avstånd till tyngdpunkten?)

Det vet vi inte med säkerhet förrän vi räknat ut dem, men vi antar att de är olika tills vidare. Det finns inget i uppgiften som säger att de är exakt lika just nu.

Med momentpunkt, är det alltså en punkt där en kraft finns, eller är det valfritt område? Vart är enklast att lägga den punkten? 

Du får välja precis vilken punkt du vill. Men det är enklare att välja en punkt i vilken en kraft angriper. Det blir enklare eftersom just den kraften får hävarmen noll (noll avstånd till momentpunkten) och då blir momentet från den kraften 0. Det ger oss alltså en enklare ekvation.

Men vi säger jag väljer punkten Fa (är vänster), så 3m.

Jättebra. Och hur lång hävarm får kraften $F_b$? Ställ sedan upp momentekvationen kring punkten $A$. Summan av alla moment kring denna punkt ska vara noll eftersom balken är i jämvikt.

Du glömde också av att svara på vad som ska gälla för kraftsumman (kraftjämvikt) Kan du teckna en ekvation för det också? Du har då sammanlagt två ekvationer och två okända.

D4NIEL skrev:

naturnatur1 skrev:

Lite slarvigt av mig! Skulle stå Fn (som normalkraft) (: men jag kallar de för f_a och f_b nu. (Hur vet vi att de inte är lika stora? Är det för att det är olika avstånd till tyngdpunkten?)

Det vet vi inte med säkerhet förrän vi räknat ut dem, men vi antar att de är olika tills vidare. Det finns inget i uppgiften som säger att de är exakt lika just nu.

Med momentpunkt, är det alltså en punkt där en kraft finns, eller är det valfritt område? Vart är enklast att lägga den punkten? 

Du får välja precis vilken punkt du vill. Men det är enklare att välja en punkt i vilken en kraft angriper. Det blir enklare eftersom just den kraften får hävarmen noll (noll avstånd till momentpunkten) och då blir momentet från den kraften 0. Det ger oss alltså en enklare ekvation.

Vad menar du med " eftersom just den kraften får hävarmen noll (noll avstånd till momentpunkten) och då blir momentet från den kraften 0" 

Hur blir den 0? Har inte vi då besvarat vilken kraft det området har? (Givetvis har den inte 0 N ,men jag fattar bara inte vad som menas med att momentet från den kraften blir till 0?)

Men vi säger jag väljer punkten Fa (är vänster), så 3m.

Jättebra. Och hur lång hävarm får kraften $F_b$?

Från Fa till Fb blir det 5m, annars från tyngdpunkt till Fb 2m

Ställ sedan upp momentekvationen kring punkten $A$. Summan av alla moment kring denna punkt ska vara noll eftersom balken är i jämvikt

Fa × 3 = 0 ?

Du glömde också av att svara på vad som ska gälla för kraftsumman (kraftjämvikt) Kan du teckna en ekvation för det också? Du har då sammanlagt två ekvationer och två okända.

 Blir det

 Fa × 3 = Fb × (2) eller (5)?

naturnatur1 skrev:

Vad menar du med " eftersom just den kraften får hävarmen noll (noll avstånd till momentpunkten) och då blir momentet från den kraften 0" 

Hur blir den 0? Har inte vi då besvarat vilken kraft det området har? (Givetvis har den inte 0 N ,men jag fattar bara inte vad som menas med att momentet från den kraften blir till 0?)

Jag är inte med på vad du menar med "område", krafterna vi arbetar med i den här uppgiften angriper i punkter, de är inte utbredda över områden.

Du måste skilja på kraft och moment. Varje kraft bidrar med ett momentet (kraften gånger hävarmen).

T.ex. blir momentet från kraften $F_g$ kraften gånger hävarmen, dvs $F_g\cdot 3\mathrm{m}\approx 6.6\mathrm{kNm}$.

Momentet från kraften $F_a$ blir kraften gånger hävarmen, dvs $F_a\cdot 0\mathrm{m}=0\mathrm{kNm}$.

Momentet från kraften $F_b$ blir kraften gånger hävarmen, dvs $F_b\cdot 5\mathrm{m}=5F_b$. Men det här kraftmomentet vill vrida balken moturs, så vi kan lägga ett minustecken framför för att visa att det vill rotera balken åt andra hållet än $F_g$

Summan av alla kraftmoment ska vara noll eftersom balken inte börjar rotera, den är i vila.

Momentet kring $A$ (som ska vara 0) blir därför

$3F_g-5F_b+F_a\cdot 0=0$

$3\cdot F_g-5\cdot F_b=0$

Ser du hur hävarmen "0" gör att $F_a$ försvinner från momentekvationen? Är du med?

D4NIEL skrev:

naturnatur1 skrev:

Vad menar du med " eftersom just den kraften får hävarmen noll (noll avstånd till momentpunkten) och då blir momentet från den kraften 0" 

Hur blir den 0? Har inte vi då besvarat vilken kraft det området har? (Givetvis har den inte 0 N ,men jag fattar bara inte vad som menas med att momentet från den kraften blir till 0?)

Jag är inte med på vad du menar med "område", krafterna vi arbetar med i den här uppgiften angriper i punkter, de är inte utbredda över områden.

Du måste skilja på kraft och moment. Varje kraft bidrar med ett momentet (kraften gånger hävarmen).

T.ex. blir momentet från kraften $F_g$ kraften gånger hävarmen, dvs $F_g\cdot 3\mathrm{m}\approx 6.6\mathrm{kNm}$.

Momentet från kraften $F_a$ blir kraften gånger hävarmen, dvs $F_a\cdot 0\mathrm{m}=0\mathrm{kNm}$.

Momentet från kraften $F_b$ blir kraften gånger hävarmen, dvs $F_b\cdot 5\mathrm{m}=5F_b$. Men det här kraftmomentet vill vrida balken moturs, så vi kan lägga ett minustecken framför för att visa att det vill rotera balken åt andra hållet än $F_g$

Förstår att formeln är M = f × r

Men fattar inte hur man ska avgöra vilket avstånd som ska sättas in för varje moment. Utgår man alltså från en momentpunkt (i detta fallet Fa) och sedan fås hävarmen genom avstånden mellan de olika punkterna? Alltså typ om jag vill ha momentet från Fg så räknar jag 

$kraften vid fg \times (avstånd från punkt fg till momentpunkt)$

Summan av alla kraftmoment ska vara noll eftersom balken inte börjar rotera, den är i vila.

Japp

Momentet kring $A$ (som ska vara 0) blir därför

$3F_g-5F_b+F_a\cdot 0=0$

$3\cdot F_g-5\cdot F_b=0$

Ser du hur hävarmen "0" gör att $F_a$ försvinner från momentekvationen? Är du med?

Jag förstår att Fa försvinner. Men jag förstår inte varför vi är intresserade av att lägga till Fg (förmodligen för de andra är okända)

Uppställningen av ekvationen är jag inte riktigt med på

naturnatur1 skrev:

Utgår man alltså från en momentpunkt (i detta fallet Fa) och sedan fås hävarmen genom avstånden mellan de olika punkterna? Alltså typ om jag vill ha momentet från Fg så räknar jag 

$kraften vid fg \times (avstånd från punkt fg till momentpunkt)$

Ja, precis så. Och du har tre krafter och därmed 3 moment, men ett av momenten blev ju som sagt 0. Så vi har egentligen bara två moment, vars summa ska vara 0.

Men jag förstår inte varför vi är intresserade av att lägga till Fg (förmodligen för de andra är okända)

Fysiken säger oss att det sammanlagda momentet av ALLA krafter ska vara 0 eftersom balken är i vila. $F_g$ är en av krafterna, därmed måste vi räkna med det moment kraften ger i momentekvationen.

D4NIEL skrev:

naturnatur1 skrev:

Utgår man alltså från en momentpunkt (i detta fallet Fa) och sedan fås hävarmen genom avstånden mellan de olika punkterna? Alltså typ om jag vill ha momentet från Fg så räknar jag 

$kraften vid fg \times (avstånd från punkt fg till momentpunkt)$

Ja, precis så. Och du har tre krafter och därmed 3 moment, men ett av momenten blev ju som sagt 0. Så vi har egentligen bara två moment, vars summa ska vara 0.

Men jag förstår inte varför vi är intresserade av att lägga till Fg (förmodligen för de andra är okända)

Fysiken säger oss att det sammanlagda momentet av ALLA krafter ska vara 0 eftersom balken är i vila. $F_g$ är en av krafterna, därmed måste vi räkna med det moment kraften ger i momentekvationen.

Jahaa!

1. Vi har alltså satt fg som (-) och fa och fb som (+) för att visa att de är åt olika riktningar? Är det själva momenten eller krafterna som bidrar till detta? Spelar det någon roll vilka som blir positiva eller negativa?

2. Det här med moment känns lite "abstrakt".. har du något vardagsexempel, eller exempel på hur "moment" används/finns omkring oss? 

Edit: typ gungbräda, vart är det momentet spelar roll? (Jag själv tänker att det mest är krafter och fattar inte vad moment har med det att göra)

3. Jag hade alltså inte kunnat sätta fg som momentpunkt? (Kan, kan man kanske, men det hade nog inte varit så smart med tanke på att vi har kraften angiven?) 

naturnatur1 skrev:

1. Vi har alltså satt fg som (-) och fa och fb som (+) för att visa att de är åt olika riktningar? Är det själva momenten eller krafterna som bidrar till detta? Spelar det någon roll vilka som blir positiva eller negativa?

2. Det här med moment känns lite "abstrakt".. har du något vardagsexempel, eller exempel på hur "moment" används/finns omkring oss?

3. Jag hade alltså inte kunnat sätta fg som momentpunkt? (Kan, kan man kanske, men det hade nog inte varit så smart med tanke på att vi har kraften angiven?) 

Krafter har en riktning och en storlek. Det naturliga brukar vara att välja uppåt (positiv y-led) som den positiva referensriktningen. Du får välja referensriktning själv, men det är viktigt att du inte byter referensriktning mitt i uppgiften.

Moment har också en sorts riktning, medurs eller moturs. Det är återigen viktigt att bestämma sig för en riktning, krafter som vill vrida något medurs kan få ge positiva moment och krafter som vill vrida moturs ger då negativa moment.

Här är en skiftnyckel som någon försöker vrida moturs. Det är lättare att hålla längre ut på handtaget eftersom anbringad kraft där ger större moment (mer hävarm).

Håll därför längre ut (angrip i punkt B) så får du längre hävarm och skapar större moment!

Du hade kunnat sätta tyngdpunkten (vid $F_g$) som momentpunkt om du kände för det. Det blir lite krångligare, men du får fortfarande två ekvationer (momentjämvikt + kraftjämvikt) och två okända.

D4NIEL skrev:

naturnatur1 skrev:

1. Vi har alltså satt fg som (-) och fa och fb som (+) för att visa att de är åt olika riktningar? Är det själva momenten eller krafterna som bidrar till detta? Spelar det någon roll vilka som blir positiva eller negativa?

2. Det här med moment känns lite "abstrakt".. har du något vardagsexempel, eller exempel på hur "moment" används/finns omkring oss?

3. Jag hade alltså inte kunnat sätta fg som momentpunkt? (Kan, kan man kanske, men det hade nog inte varit så smart med tanke på att vi har kraften angiven?) 

Krafter har en riktning och en storlek. Det naturliga brukar vara att välja uppåt (positiv y-led) som den positiva referensriktningen. Du får välja referensriktning själv, men det är viktigt att du inte byter referensriktning mitt i uppgiften.

Moment har också en sorts riktning, medurs eller moturs. Det är återigen viktigt att bestämma sig för en riktning, krafter som vill vrida något medurs kan få ge positiva moment och krafter som vill vrida moturs ger då negativa moment.

Här är en skiftnyckel som någon försöker vrida moturs. Det är lättare att hålla längre ut på handtaget eftersom anbringad kraft där ger större moment (mer hävarm).

Håll därför längre ut (angrip i punkt B) så får du längre hävarm och skapar större moment!

Du hade kunnat sätta tyngdpunkten (vid $F_g$) som momentpunkt om du kände för det. Det blir lite krångligare, men du får fortfarande två ekvationer (momentjämvikt + kraftjämvikt) och två okända.

Jahaa!

En sista fråga, är det rätt tankesätt?

nu är fa cirka 1,3kN.  Kraften nedåt var fg som ungefär är 2,2kN. Nu ska dessa subtraheras för att få ut Fb?

Edit: utan avrundning påvägen förstås

Gungbräda: vad som händer beror på hur långt från mitten man sitter. En vuxen och ett barn kan gunga tillsammans om den vuxne sitter närmare mitten än barnet gör.

naturnatur1 skrev:

Jahaa!

En sista fråga, är det rätt tankesätt?

nu är fa cirka 1,3kN.  Kraften nedåt var fg som ungefär är 2,2kN. Nu ska dessa subtraheras för att få ut Fb?

Edit: utan avrundning påvägen förstås

Ja, men jag tror tror du har blandat ihop $F_a$ och $F_b$, det är $F_b=\frac35mg\approx 1.3\mathrm {kN}$

Den sista kraften $F_a$ får vi sedan från kraftjämvikten. Eftersom balken ligger stilla måste summan av alla krafter bli noll.

$F_a-F_g+F_b=0$

$F_a=F_g-F_b=\frac25mg\approx 880\mathrm{N}$

Ett annat sätt att säga det är att balkens tyngd måste bäras upp av de två bockarna. $F_g=F_a+F_b$.

D4NIEL skrev:

naturnatur1 skrev:

Jahaa!

En sista fråga, är det rätt tankesätt?

nu är fa cirka 1,3kN.  Kraften nedåt var fg som ungefär är 2,2kN. Nu ska dessa subtraheras för att få ut Fb?

Edit: utan avrundning påvägen förstås

Ja, men jag tror tror du har blandat ihop $F_a$ och $F_b$, det är $F_b=\frac35mg\approx 1.3\mathrm {kN}$

Den sista kraften $F_a$ får vi sedan från kraftjämvikten. Eftersom balken ligger stilla måste summan av alla krafter bli noll.

$F_a-F_g+F_b=0$

$F_a=F_g-F_b=\frac25mg\approx 880\mathrm{N}$

Ett annat sätt att säga det är att balkens tyngd måste bäras upp av de två bockarna. $F_g=F_a+F_b$.

Jag skrev lite fel här. Räknade om och ja jag menar att fb är 1,3kN. Tusen tack för hjälpen!

En mer allmän fråga ang uppgiften.

Förstår inte riktigt hur moment utövas här? (Mer än att det är punkter och avstånd) men fattar inte vad det är vi skulle kunna vrida medurs eller moturs? 

Eller ville man bara räkna ut krafterna (mha moment?)

Vi använder momentjämvikt för att beräkna krafterna.

Tänk dig att du ser balken ligga på de två bockarna och så plötsligt försvinner bocken vid stödjepunkt B.

Vad skulle hända då? Skulle balken börja rotera åt något håll?

D4NIEL skrev:

Vi använder momentjämvikt för att beräkna krafterna.

Tänk dig att du ser balken ligga på de två bockarna och så plötsligt försvinner bocken vid stödjepunkt B.

Vad skulle hända då? Skulle balken börja rotera åt något håll?

Nedåt, alltså medurs? 

Ja, balken skulle ramla ned, rotera medurs tills den slår i marken.

Det beror på att momentet som tyngdkraften skapar runt A inte längre balanseras. Alltså börjar balken rotera kring A.

D4NIEL skrev:

Ja, balken skulle ramla ned, rotera medurs tills den slår i marken.

Det beror på att momentet som tyngdkraften skapar runt A inte längre balanseras. Alltså börjar balken rotera kring A.

Tack för hjälpen och utförliga svar!(:

"Att något är homogent innebär det att föremålet har samma densitet överallt och detta innebär i sin tur att tyngdkraften kan antas angripa i föremålets tyngdpunkt som då är i mitten av brädan."

Gäller detta alltid? Bildas det alltså en "ny punkt" på föremålet? (Som gör att man delar hela längden/hävarmen på 2? ) [Här behövdes det väl inte eftersom vi hade längderna på vardera sida utgivna?]