b) uppgiften

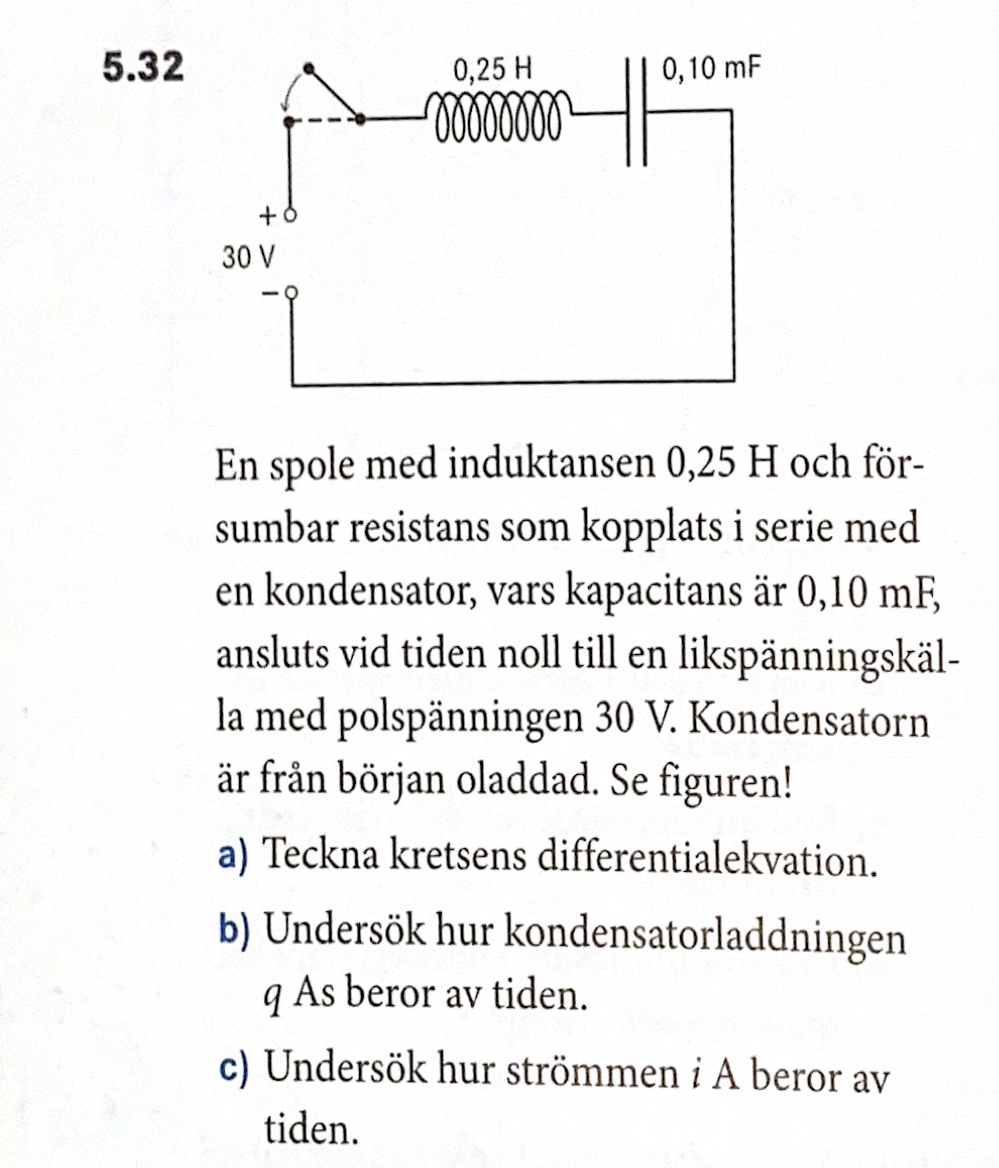
från a ) får jag att diff.ekvationen är 

$\frac{d^{2}q}{a{t}^2}+$$4\times {10}^{4}q$ =120

lösningen består av en homogen, q_h och en partikulära lösning q_p

q_h = Asinωt + Bcosωt 

q'_h =ωAcosωt - Bωsinωt

q''_h =-Aω²sinωt - Bω²cosωt

-Aω²cosωt - Bω²sinωt + 4×10⁴q ( Asinωt + Bcosωt ) = ?

Vet inte rikitgt vad HL ska ha för värde, jag vet ju att laddningen har lösningen q =- $\hat{q}$ cosωt där $\hat{q}$= $\hat{u}\times C$ och vi har ju effektivvärdet som är U = 30V där U= $\frac{\hat{u}}{\sqrt{2}}$

$\hat{q}$ blir därför $\hat{q}=\left(30\times \sqrt{2}\right)\times$0,0001 men problemet är när jag arbetar med VL . Det finns ju inte sinωt därmed blir A = 0. men ω ges av $\sqrt{\frac{1}{LC}}$ som är 200 och ω² = 4×10⁴

 - 4×10⁴cosωt + 4×10⁴ Bcosωt ) = - $\hat{q}$ cosωt 

får vi att VL=0