Avståndsformeln.

Välkommen till Pluggakuten! När man inte direkt kommer på lösningen är det alltid bra att rita en bild:

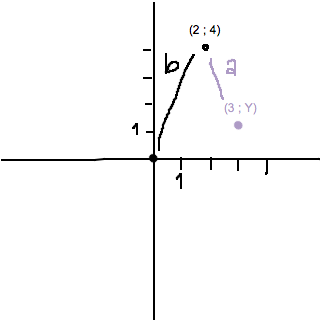
Avståndet a ska vara lika stort som avståndet b. Avståndsformeln är helt rätt tanke! Hur stort är avståndet från (2;4) till origo? Hur stort är avståndet från (2;4) till (3;Y)? Kommer du vidare?

 Avståndet från (2;4) till origo är $\sqrt{20}$ men sen kan jag inte lösa mer.

Då måste avståndet från vår punkt till (2;4) också vara $\sqrt(20)$! Avståndet i x-led är ett. Då kan vi skriva att:

$\sqrt(20)=\sqrt((2-3)^{2}+(4-Y)^{2})$

Kan du lösa det? 

Kanske kommer in och stör här, men om jag läser uppgiften som en svensklärare tolkar jag det som att det är avstånden $a$ och $c$ som ska vara lika ($c$ är avståndet från punkten $(3,Y)$ till origo).

tomast80 skrev :

Kanske kommer in och stör här, men om jag läser uppgiften som en svensklärare tolkar jag det som att det är avstånden $a$ och $c$ som ska vara lika ($c$ är avståndet från punkten $(3,Y)$ till origo).

Här skulle jag inte hålla med. Det står att punkten (3;Yär lika långt bort från origo, som från punkten (2;4). 

Smutstvätt skrev :

tomast80 skrev :

Kanske kommer in och stör här, men om jag läser uppgiften som en svensklärare tolkar jag det som att det är avstånden $a$ och $c$ som ska vara lika ($c$ är avståndet från punkten $(3,Y)$ till origo).

Här skulle jag inte hålla med. Det står att punkten (3;Yär lika långt bort från origo, som från punkten (2;4). 

Det är det som tomast80 skriver också. Det är inte det du har ritat. Du har ritat att punkten (2,4) är lika långt från origo som från (3,y).

Aj, fasiken! Det var slarvigt av mig. Korrekt illustration:

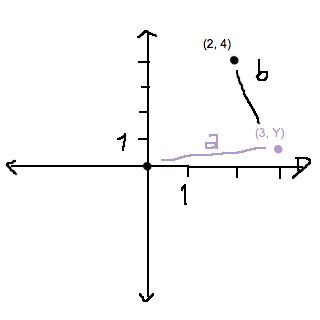
Jag ber om ursäkt.

Ingen fara! Ursäkten accepterad!

Alternativ lösning:

$c$ är tredje sidan, mellan origo och punkten $(2,4)$. Om vi utgår från mittpunkten från den sidan och drar en linje som är vinkelrät mot $c$ så har den följande ekvation, enligt enpunktsformeln:

$y-y_1=k(x-x_1)$

Eftersom $(x_1,y_1)$ är mittpunkten på sidan $c$ fås:

$x_1 = 1$, $y_1 = 2$

$k\cdot 2 = - 1 \Rightarrow$

$k = -\frac{1}{2}$

Eftersom linjen är vinkelrät mot $c$.

Vi kan skriva om linjen på formen:

$y = kx-kx_1+y_1$

$y = -\frac{x}{2}+\frac{1}{2}+2$

$y = -\frac{x}{2}+\frac{5}{2}$

Slutligen söker vi värdet på $y$ då $x=3$:

$y = -\frac{3}{2}+ \frac{5}{2} = ...$

Tyvärr grepar jag det inte iallafall. 

Blandis00 skrev :

Tyvärr grepar jag det inte iallafall. 

Om någon kan rita en snygg bild (hinner inte nu) klarnar nog lösningen. Det blir nämligen en likbent triangel där den nya linjen är ”höjden” mot sidan $c$. Kan någon annan förklara bättre?