Avstånd mellan två punkter i en graf och en rät linje
Hej,
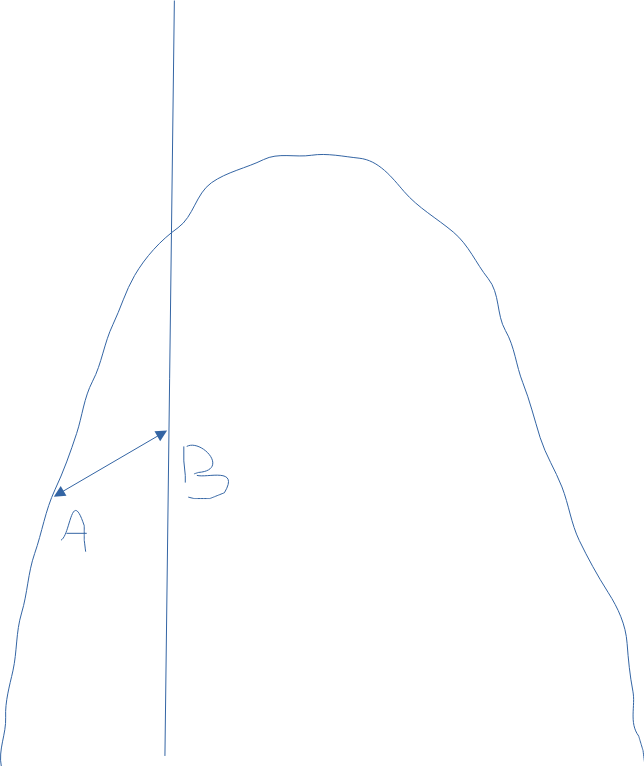
Här är funktionerna y=f(x) och den räta linjen g(x) utritade.
Vad är uttrycket för avståndet mellan punkterna A och B?
Minsta respektive längsta avstånd? Beräkning?
Det är f(x)-g(x) som ska tas väl, men vet inte vad funktionerna har för värde (hur dem ser ut/går). Kan man komma fram till något ändå dvs hur man kommer fram till avståndet och uttrycket för detta? Minsta,respektive längsta avstånd?
Det finns något som heter avståndsformel, är inte så insatt i denna, men ska den tillämpas här?
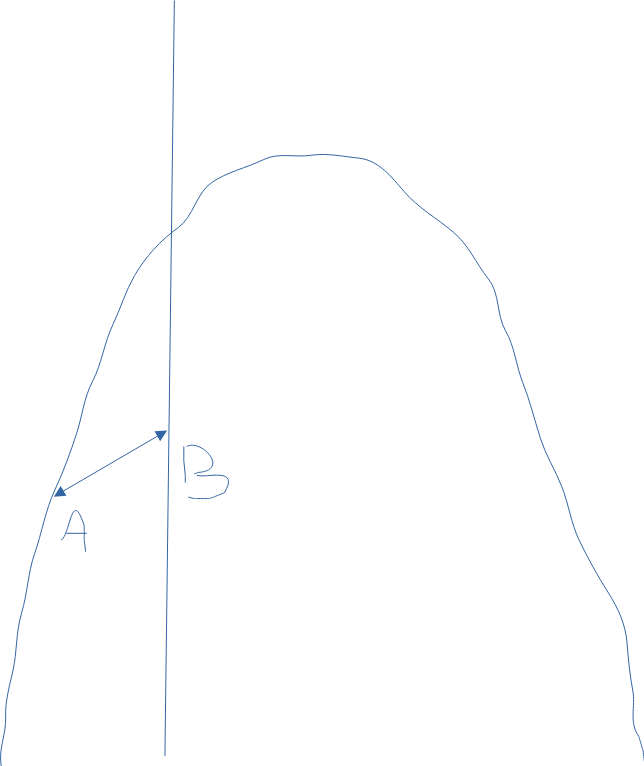
Har du en bild på hela uppgiften? Känns konstigt om det där var all info man gav ut och förväntar att man ska räkna ut kortaste/längsta avstånd.
Henrik 2 skrev:,Här är funktionerna y=f(x) och den räta linjen g(x) utritade.
Vad är uttrycket för avståndet mellan punkterna A och B?
Här kan du använda avståndsformeln direkt, se nedan.
Minsta respektive längsta avstånd? Beräkning?
Det är f(x)-g(x) som ska tas väl,
Nej, f(x) - g(x) beskriver endast skillnaden i y-led vid en viss x-koordinat
men vet inte vad funktionerna har för värde (hur dem ser ut/går). Kan man komma fram till något ändå dvs hur man kommer fram till avståndet och uttrycket för detta?
Det blir väldigt teoretiskt och abstrakt om vi försöker beskriva minsta/största avståndet utan att veta mer om f(x), g(x) och vilket intervall som är intressant.
Det finns något som heter avståndsformel, är inte så insatt i denna, men ska den tillämpas här?
Ja, den kan användas för att bestämma avståndet mellan två punkter i ett koordinatsystem.
Läs mer om den här och fråga sedan oss om allt du vill att vi förklarar närmare.
Som det ser ut i din bild så skär graferna varandra i en punkt.
Då kan vi direkt, utan några beräkningar, säga att det minsta avståndet är 0.
Vad gäller det största avståndet så är det lite mer osäkert.
Om den ena grafen är en parabel och om vi inte har något givet intervall att förhålla oss till (dvs att graferna fortsätter att sträcka ut sig obegränsat) så gäller det att avståndet mellan graferna bara växer och växer obehindrat ju längre bort från skärningspunkten vi kommer.
I så fall finns det inte något största avstånd mellan graferna.
=====
För att kunna säga något vettigt kring problemet så behöver vi alltså veta mer om f(x), g(x) och eventuellt intervall.
Hej,
Ok, men då jag inte har någon mer info om funktionerna kan vi antingen ta det hypotetiskt/fiktivt eller skapa två funktoner av f(x) o g(x) så jag lär mig principen, det e det viktigaste.
Man behöver även för att komma fram till avståndet mellan a o b med hjälp av avståndsformeln veta vad x o y är . Om det inte framkommer i en uppgift kan man komma fram till något ändå?
Ok, denna formel e kopplad till pythagoras sats där man drar sk hjälplinjer till punkerna a o b så det blir c o d punker också, där sidan d e hypotenusan och den används för att ta roten ur. Hade et tal om det med silverplatta o guldtråd så liknande men bara här har jag inte några siffror att beräkna det med.
Just det, dem skär varandra då är det där det minsta avståndet är såklart men sedan det längsta/största?
O om dem fortsätter att växa så blir avstpndet bara längre o längre.
Mvh/H
Är avståndsformeln med bara detta uttryck mellan a o b o punkter c o d som man kan rita ut, som jag inte gjort. Då blir AC kateter o BC den andra katetern och D blir hypotenusan
AC2 +BC2 =D2
D=√AC2 +BC2
Kan man beräkna avståndet i denna om man inte har mer att gå efter?
Mvh/H
Henrik 2 skrev:Är avståndsformeln med bara detta uttryck mellan a o b o punkter c o d som man kan rita ut, som jag inte gjort. Då blir AC kateter o BC den andra katetern och D blir hypotenusan
AC2 +BC2 =D2
D=√AC2 +BC2
Kan man beräkna avståndet i denna om man inte har mer att gå efter?
Mvh/H
Vad är a, b, c d, A, B, C och D?
Man gör en rektangel mellan avståndet a till b med hälp av sk hjälp/stödlinjer o får dessa punkter o sedan så är det ju så avståndsformel är såg jag?
Mvh/H
Nej, du ska rita en rätvinklig triangel, inte en rektangel.
Vi vill veta avståndet mellan punkt A och punkt B.
Se bild:

Vi ritar då en horisontell hjälplinje frän A till C och en vertikal hjälplinje från B till C.
Låt nu
- c vara längden av sträckan AB
- a vara längden av sträckan BC
- b vara längden av sträckan AC
Då gäller enligt Pythagoras sats att c2=a2+b2, dvs c=√a2+b2.
Så långt är du med hoppas jag.
Vi säger nu att koordinaterna för punkt A är (x1,y1) och att koordinaterna för punkt B är (x2,y2).
Då är a=y2-y1 och b=x2-x1.
Vi kan då uttrycka Pythagoras sats med hjälp av dessa koordinater, vilket ger oss avståndsformeln c=√(y2-y1)2+(x2-x1)2.
Sorry, menade rätvinklig triangel, det var faktiskt det jag menade, my bad..:)
Kikar din beräkning,tackar.
/H
E med på detta.
Tack/H
Denna e som den med silverplatta o guldtråd med ett min av guldtråd.
Bra att du ser samband mellan uppgifter och metoder.
Vill du att vi jobbar vidare med denna uppgift?
Yes, det vill jag gärna. Så vad mer kan tolkas/göras/beräknas?
Mvh/H
Så vad mer kan göras o tolkas i denna uppgift?
Vi har gått igenom avståndsformeln o mer?
Mvh/H
"Bump" vill o behöver jobba vidare med uppgiften. Vad mer kan tolkas/göras?
Mvh/H
Jag tror att du på gymnasienivå endast behöver lösa uppgifter av detta slaget där de frågar efter det vertikala avståndet mellan de två graferna, dvs |f(x)-g(x)| i ett givet intervall [a, b].
Då kan du lösa uppgiften genom att bilda en ny funktion h(x) = f(x) - g(x) och sedan fortsätta lösningen på olika vägar beroende på om h(x) har nollställe eller inte i aktuellt intervall:
Alternativ 1: h(x) har nollställen.
Då är det minsta avståndet mellan graferna lika med 0 och det största avståndet återfinns vid antingen h(a), h(b) eller vid den/de punkter där h'(x) = 0 i det aktuella intervallet.
Alternativ 2: h(x) saknar nollställen
Då återfinner du både det minsta och det största avståndet mellan graferna vid h(a), h(b) eller vid den/de punkter där h'(x) = 0 i det aktuella intervallet
Hej Y,
För att jag ska kunna förstå vad du menar, kan du rita upp detta med h(x)= f(x)-g(x) o de alternativa vägarna så jag ser,blir enklare att förstå det då?
Mvh/H
Försök själv med dessa två fall:
- Fall 1: f(x) = x2 och g(x) = x-4
- Fall 2: f(x) = x2 och g(x) = x+2
Nej, jag förstår inte o ser inte hur man ska göra.
Mvh/H
Vad av följande är det du inte förstår?
Vi tar fall 1 som exempel och väljer intervallet [-2, 2]
- f(x)=x2 och g(x)=x-4
- Skillnaden mellan dessa funktioner ör h(x) = f(x)-g(x) = x2-(x-4) = x2-x+4
- Nollställena till h(x) fås genom att lösa ekvationen x2-x+4 = 0
- Ekvationen saknar lösning, vilket gör att nollställen saknas.
- Det betyder att graferna inte skär varandra
- Det betyder att det minsta avståndet mellan graferna är större än noll
- För att hitta största/minsta avståndet letar vi nu efter eventuella minimi-/maximipunkter till h(x) I intervallet.
- Därför deriverar vi h(x), villet ger oss h'(x) = 2x-1.
- h'(x) = 0 ger oss ekvationen 2x-1 = 0, med lösning x = 1/2.
- Denna lösning ligger i det tillåtna intervallet [-2, 2].
- Kandidater till största och minsta avstånd är därför vid x = -2, vid x = 1/2 och vid x = 2
- Vi har att h(-2) = (-2)2-(-2)+4 = 10, h(1/2) = (1/2)2-1/2+4 = 3,75 och h(2) = 22-2+4 = 6.
- Vi ser att det minsta avståndet är 3,75 och det största avståndet är 10.
Ok, tack för förklaring, skulle inte kunna detta själv.
h,b o h,a e alltså de punkter A och B som e utritade i inlägg 1?
Mvh/H
Henrik 2 skrev:Ok, tack för förklaring, skulle inte kunna detta själv.
Efter lite träning så kommer du att kunna det.
h,b o h,a e alltså de punkter A och B som e utritade i inlägg 1?
Nej, istället är det så här (se bild):
- Det största vertikala avståndet mellan graferna är 10 längdenheter (mellan A och B, vid x = -2).
- Det minsta vertikala avståndet mellan graferna är 3,75 längdenheter (mellan C och D, vid x = 0,5)

Hej,
Ok, ser att det e ett vertikalt avstånd på dessa mått, dv s största o minsta längdenheter. Men om man utgår från den bild som jag hade i inlägg 1 och du gjorde/ritade i hur tolkar man dessa grafer jämfört med den?
f(x) är ju ritad här tvärtom o den räta linjen g(x) är ju här diagonal det var den inte som jag ritade. Är det för att du tog dessa funktioner som du hittade på f(x)=x2 och g(x)=x-4?
Kan du förklara hur man ser att dem går som dem gör i grafen.
Mvh/H
P.s Ja övning ger färdighet,men vi alla förstår olika snabbt/långsamt dock. Men det e övning som gäller,speciellt i matte..som gemene man inte förstå,specielt när man ska tillämpa saker o ting o lösa problem,vet som oftast inte hur man löser dem.
Henrik 2 skrev:Hej,
Ok, ser att det e ett vertikalt avstånd på dessa mått, dv s största o minsta längdenheter. Men om man utgår från den bild som jag hade i inlägg 1 och du gjorde/ritade i hur tolkar man dessa grafer jämfört med den?
I svar #16, #18, #20 och #22 så har jag hittat på en enklare uppgiftslydelse eftersom jag tror att det är det du behöver träna på, åtminstone inledningsvis. Jag har hittat på två funktioner f(x) och g(x) för att det ska gå att få till en konkret lösning och sä attvi inte behöver försöka beskriva generella lösningsmetodrer.
Även detta eftersom jag tror att det är enklare för dig att ta till dig metoden om den inte är så abstrakt.
Så det är en annan frågeställning och andra grafer jämfört med ditt inlägg #1. Därför går de inte att jämföra.
f(x) är ju ritad här tvärtom o den räta linjen g(x) är ju här diagonal det var den inte som jag ritade. Är det för att du tog dessa funktioner som du hittade på f(x)=x2 och g(x)=x-4?
Ja, jag hittade på funktioner för att det skulle bli konkret.
Kan du förklara hur man ser att dem går som dem gör i grafen.
Jag använde det digitala onlineverktyget Desmos för att rita graferna.
Men du bör träna på att grovt skissa grafer som dessa för hand.
Det sparar mycket tid och underlättar både innan, under och efter en problemlösning.
Ok, tack, jag kan inte o förstår inte om man får/har en funktion hur den går, ser inte o har inte lärt mig det. Så kan du, någon förklara konkret o ge mig exempel så jag förstår hur grafen går vid en specifik funktion. Jag förstår ungefär hur den går när det e 1a gradare, rät linje, 2a gradare, 3dje gradare...Men om man skriver en funktion f(x)=........ så kan jag inte förstå hur man ritar in den o se hur grafen går.
Så om någon kunde ge mig konkret exempel här så jag kan få en lite mer förståelse för detta.
Mvh/H
Henrik 2 skrev:Ok, tack, jag kan inte o förstår inte om man får/har en funktion hur den går, ser inte o har inte lärt mig det. Så kan du, någon förklara konkret o ge mig exempel så jag förstår hur grafen går vid en specifik funktion. Jag förstår ungefär hur den går när det e 1a gradare, rät linje, 2a gradare, 3dje gradare...
I det här fallet var det ju dels en rät linje (graf till en linjär funktion) och en enkel parabel (graf till en andragradsfunktion), så de bör du kunna skissa för hand.
Men om man skriver en funktion f(x)=........ så kan jag inte förstå hur man ritar in den o se hur grafen går.
Så om någon kunde ge mig konkret exempel här så jag kan få en lite mer förståelse för detta.
Läs gärna detta avsnitt för lite tips.
Och, om du vill, även detta avsnitt för lite mer komplicerade funktioner.
Ok, förstår räta linjen, 1a gradare och 2a gradare parabel. Är en 2a gradare alltid en parabel?
Kikar avsnittet.
Mvh/H
Ok, som ett exempel på en lätt o konkret funktion x2 -x-2
x2 så ser man att det är en andragradare/parabel?
-x är att den går neråt med en minpunkt?
-2=m=y= var den skär y axeln?
Mvh/H
Henrik 2 skrev:[...]
Är en 2a gradare alltid en parabel?
Ja.
Henrik 2 skrev:Ok, som ett exempel på en lätt o konkret funktion x2 -x-2
x2 så ser man att det är en andragradare/parabel?
Ja, och eftersom koefficienten framför x2-termen är positiv så vet vi även att den har formen av en "smilie face" samt att parabeln därför har en minimipunkt.
-x är att den går neråt med en minpunkt?
Nej, termen -x indikerar att symmetrilinjen ligger vid x = -o/2 = -(-1)/2 = 1/2.
-2=m=y= var den skär y axeln?
Ja, termen -2 indikerar att parabeln skär y-axeln vid y = -2. Men detta kallas inte för m-värde utan istället p (ftån pq-formeln) eller c (från abc-formeln/lösningsformeln).
Tillägg: 7 jun 2024 07:39
Nu skrev jag fel. Konstanttermen -2 kan
- kallas q om andrgradsuttrycket är skrivet på formen x2+px+q
- kallas c om andragradsuttrycket är skrivet på formen ax2+bx+c