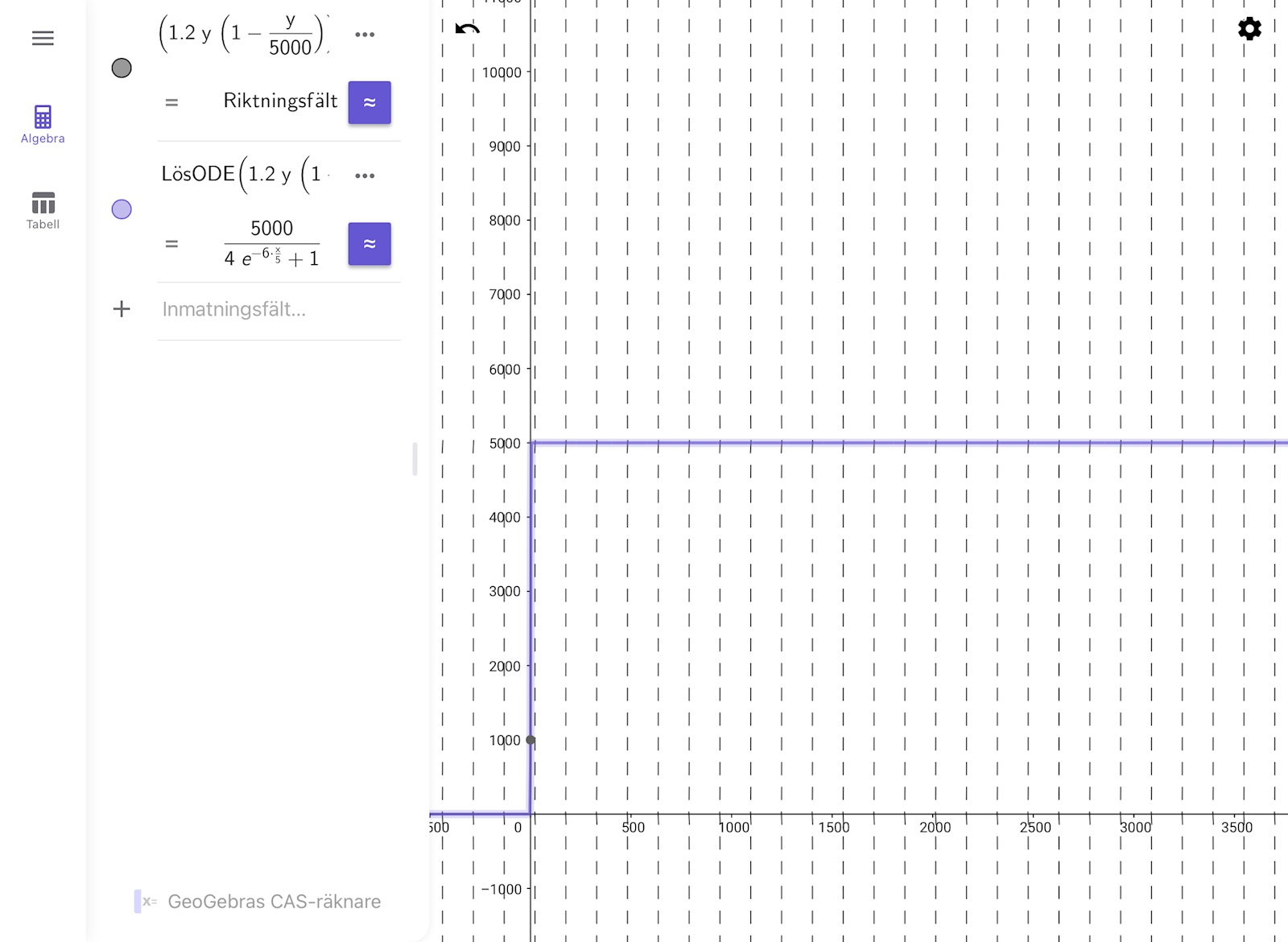
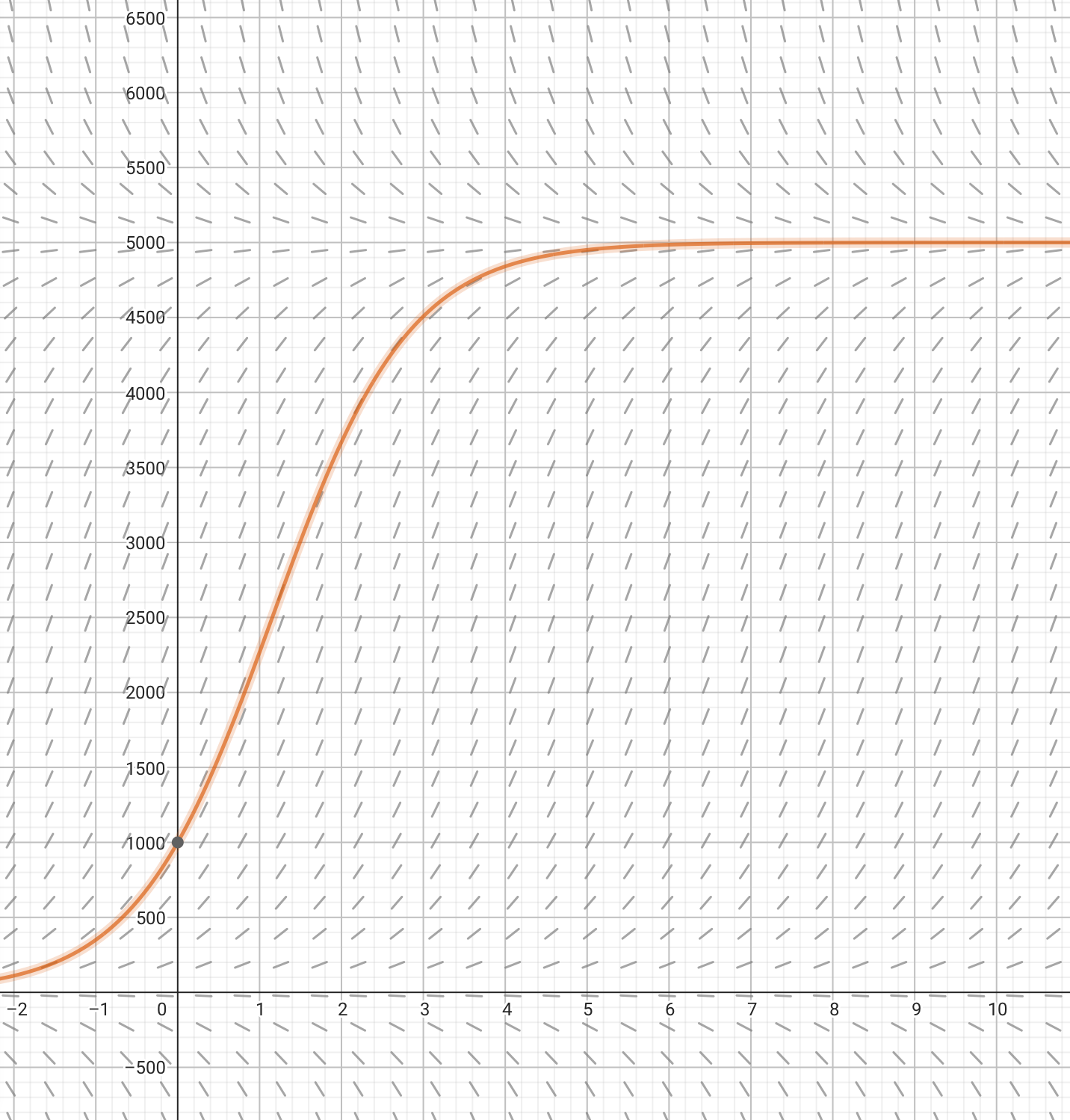
avläsa riktningsfält b) uppgiften

I facit står det att jag m.h.a. rita ett riktningsfält kan lösa frågan
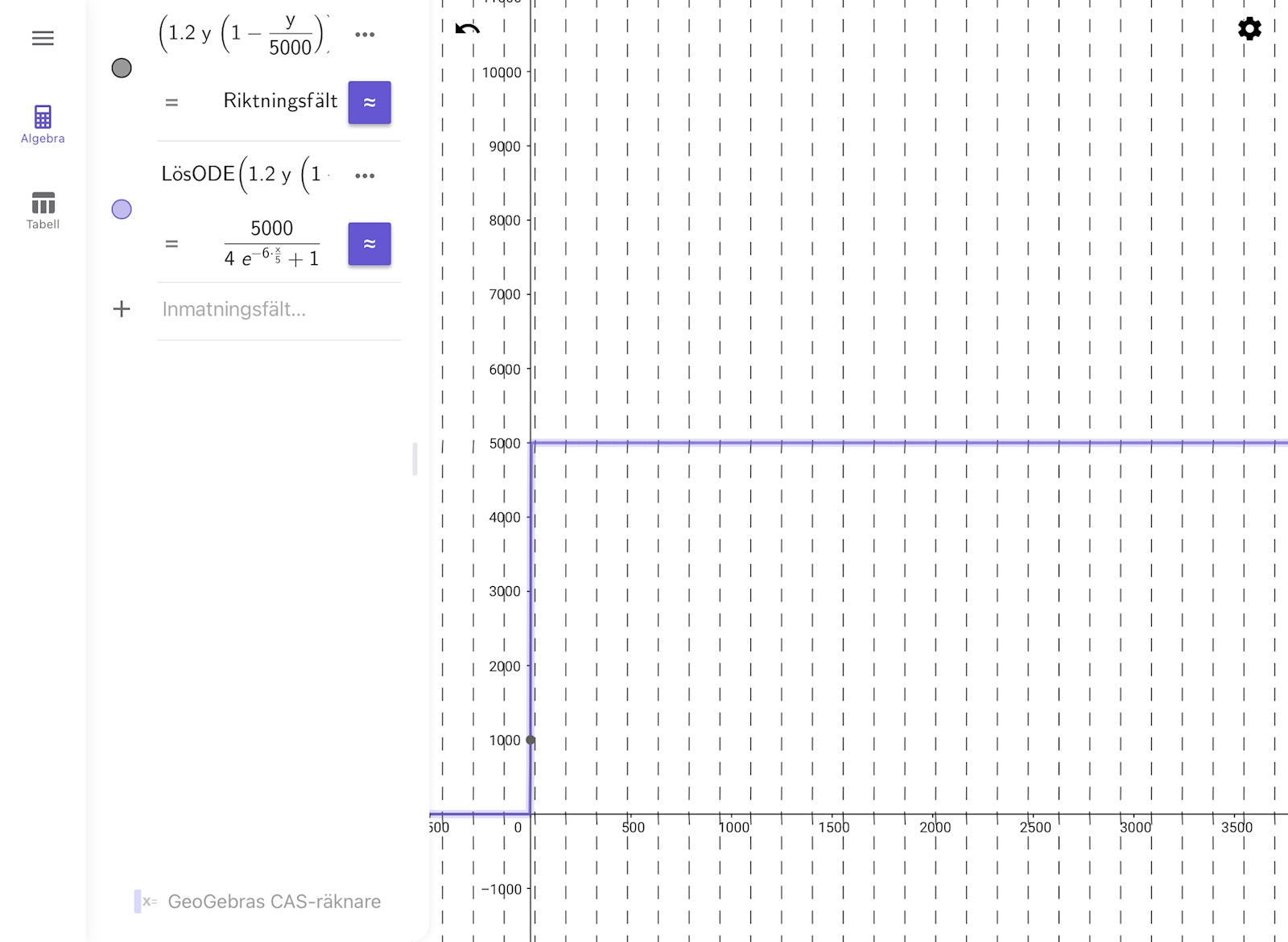
jag visste utan att behöva rita att y'har sitt max då y M och sen avtar populationensstorlek men hur kan jag se det i grafen?
fysik3 skrev:
I facit står det att jag m.h.a. rita ett riktningsfält kan lösa frågan
jag visste utan att behöva rita att y'har sitt max då y M och sen avtar populationensstorlek men hur kan jag se det i grafen?
Hur definierar du M?
hur menar du? M=populationens maximala storlek och är i detta fal 5000
Om du ändrar skalan på t-axeln så ser man bättre hur det ser ut nära t = 0.
Redan för t = 10 så är riktningen nästan vertikal: där är den ungefär 12.
Låt tiden gå upp till 1 i stället.
fysik3 skrev:
ja nu ser jag att då värdet på y >5000 går strecken ner, är det så jag ska tänka?
Ja. Det framgår direkt av ekvationen också.
fysik3 skrev:hur menar du? M=populationens maximala storlek och är i detta fal 5000
Hur skulle jag kunna gissa det när du inte har skrivit det?
Laguna skrev:Ja. Det framgår direkt av ekvationen också.
ja av ekvationen förstod jag. Behövde justera axlarna så jag kunde se riktingsfältet bättre
Smaragdalena skrev:fysik3 skrev:hur menar du? M=populationens maximala storlek och är i detta fal 5000
Hur skulle jag kunna gissa det när du inte har skrivit det?
i ekvationen avslöjas det genom att vi vet att den logisitiska tillväxrmodellen är
där M är populationens maximala storlek, utifrån ekvationen är 5000=M. Vet inte om det finns olika logisitiska tillväxtmodeller men det är denna vi jobbar med