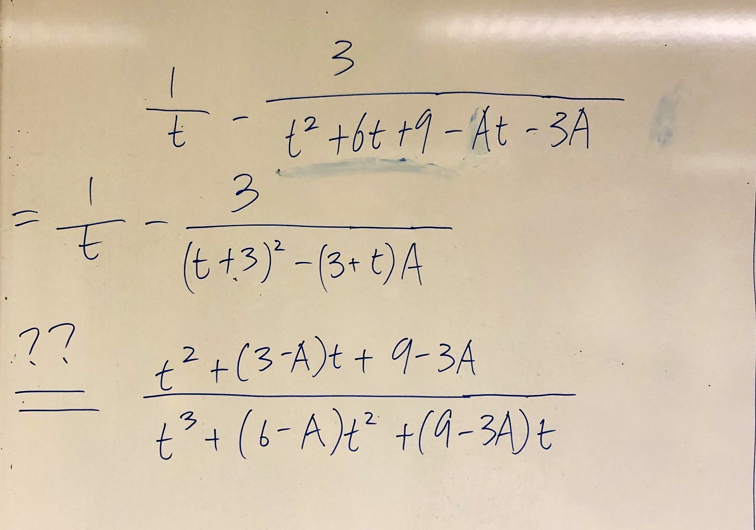Avgör konstanten så gränsvärde existerar och är ändligt

Man kan skriva om hela gränsvärde så här:

$\underset{x\to 3}{\lim }\left(\frac{1}{x-3}\right)-\underset{x\to 3}{\lim }\left(\frac{3}{x^2-Ax}\right)$

$$\begin{gathered} x-3=t \\ \frac{1}{t}-\frac{3}{t^2+6t+9-At-3A}=\frac{t^2+(3-A)t+9-3A}{t^3+(6-A)t^2+(9-3A)t} \\ Fall 1: A\ne 3 : Gränsvärdet går mot oändligheten då t\to 0. \\ Fall 2: A=3 : \\ \frac{t^2}{t^3+3t^2}=\frac{1}{t+3}\to \frac{1}{3} då t\to 0. \end{gathered}$$

Hur visst du att A=3 ?

Om $A\ne 3$ blir den första termen oändlig, men den andra ändlig. Bara om $A=3$ kan differensen av termerna bli ändlig.

tomast80 skrev:

Om $A\ne 3$ blir den första termen oändlig, men den andra ändlig. Bara om $A=3$ kan differensen av termerna bli ändlig.

Okej, nu hänger jag med, därför ska man inte skriva om dem till två separerat uttryck.

andreaas10 skrev:

$$\begin{gathered} x-3=t \\ \frac{1}{t}-\frac{3}{t^2+6t+9-At-3A}=\frac{t^2+(3-A)t+9-3A}{t^3+(6-A)t^2+(9-3A)t} \\ Fall 1: A\ne 3 : Gränsvärdet går mot oändligheten då t\to 0. \\ Fall 2: A=3 : \\ \frac{t^2}{t^3+3t^2}=\frac{1}{t+3}\to \frac{1}{3} då t\to 0. \end{gathered}$$

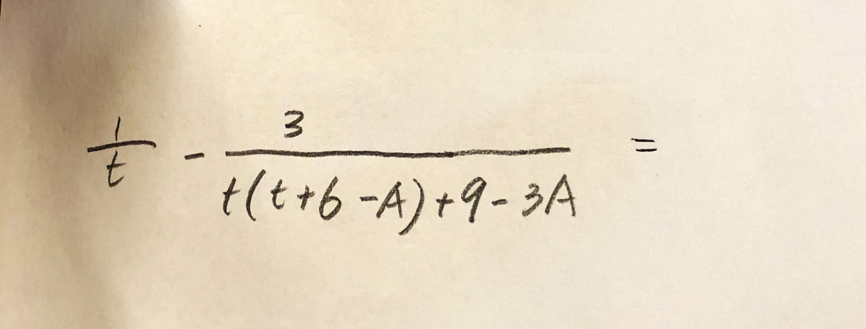
Jag förstår inte hur du har kommit fram till den sista uttrycket.