Avbildningsmatris till en projicering
Let beta be the standard basis for H and H:R² --> R². Compute H where H is the transformation that projects each vector along v=(1,2) on the vector space M={(1,1)}.
Här är lärarens lösning men jag förstår inte varför H(v) = 0 ? Menar de inte att alla vektorer som är längs med v projiceras på vektorrummet M? I så fall hur kan H(v) = 0 ?
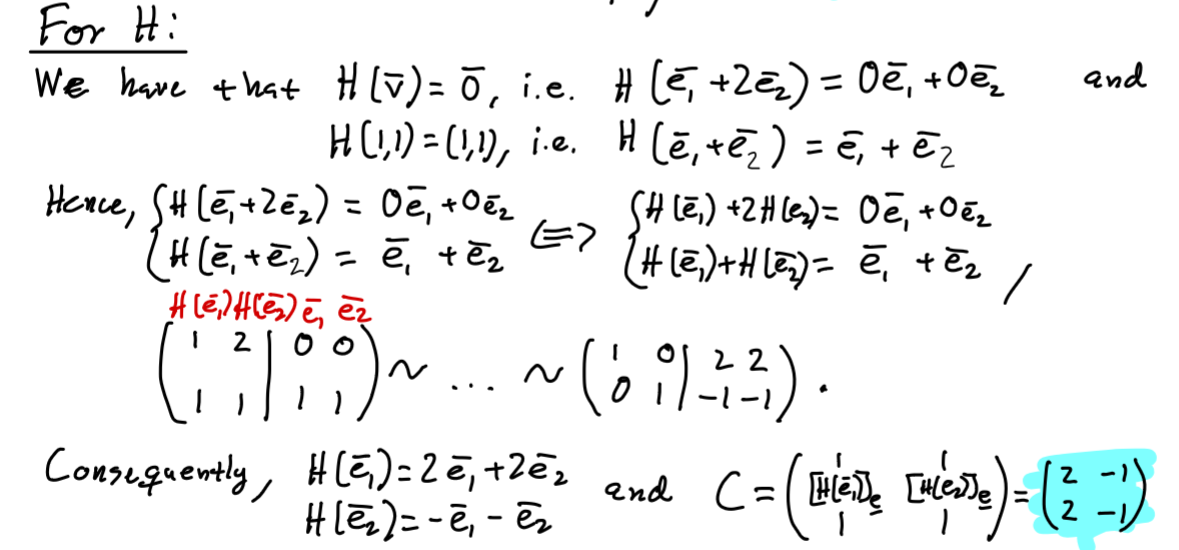
Jag håller med dig och begriper inte hur din lärare har tänkt. Inte ens då jag tittar på hur som läraren gjort och försöker röna ut vad hen kan ha menat så känner jag att jag blir klokare.
Det enda som jag tänker är att de kanske menar att man skall ta bort de bitar i vektorn som ligger längs med v tills att man når M, men då (1,1) har en viss utsträckning i (1,2)-led så förstår jag inte varför man kan anta att den projiceras på sig själv.
Säg att du har två linjärt oberoende vektorer a och b i R2. Dvs en bas.
Varje vektor x kan då skrivas som en (unik) linjärkombination.
x = ca + db, där c och d är skalärer, som naturligtvis beror av x.
Med projektionen av x på a längs b menar vi avbildningen
H(x) = H(ca + db) = ca.
Detta definierar en linjär avbildning. (Övertyga dig om att så är fallet.)
Uppenbarligen gäller det nu att
H(a) = H(1a + 0b) = 1a = a.
H(b) = H(0a + 1b) = 0a = 0.
Det är detta som utnyttjas för att hitta hur avbildningen H avbildar standardbasen, vilket i sin tur hjälper oss att ställa upp avbildningens standardmatris.
PATENTERAMERA skrev:Säg att du har två linjärt oberoende vektorer a och b i R2. Dvs en bas.
Varje vektor x kan då skrivas som en (unik) linjärkombination.
x = ca + db, där c och d är skalärer, som naturligtvis beror av x.
Med projektionen av x på a längs b menar vi avbildningen
H(x) = H(ca + db) = ca.
Detta definierar en linjär avbildning. (Övertyga dig om att så är fallet.)
Uppenbarligen gäller det nu att
H(a) = H(1a + 0b) = 1a = a.
H(b) = H(0a + 1b) = 0a = 0.
Det är detta som utnyttjas för att hitta hur avbildningen H avbildar standardbasen, vilket i sin tur hjälper oss att ställa upp avbildningens standardmatris.
Det som jag missförstod är att jag blandade ihop ortogonal projicering med icke-ortogonal porojicering. Frågan handlar om en icke-ortogonal projicering av vektorer längs med v på M. Nu förstår jag varför H(v) = 0.
Men tack för din förklaring också.



