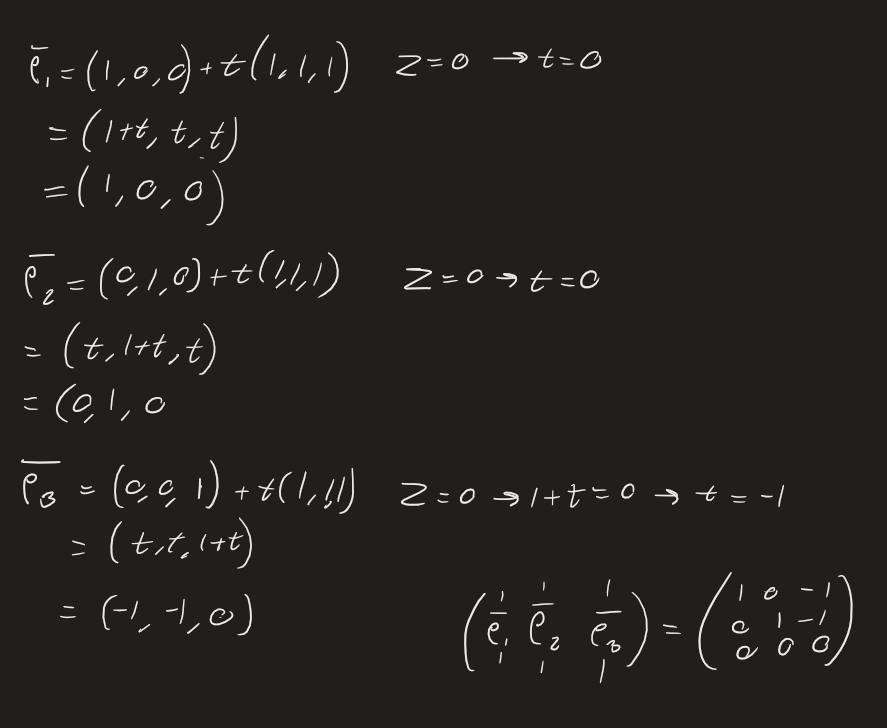Avbildningsmatris som motsvarar sned projektion

Ett sätt att se på saken är följande:

Du kommer i slutändan ha avbildningsmatrisen A.

$A=\left(\begin{array}{ccc}{a}_{11}& a_{21}& a_{31}\\ a_{12}& a_{22}& a_{32}\\ a_{13}& a_{23}& a_{33}\end{array}\right)$

Vad händer om man applicerar denna på en av våra basvektorer, t.ex. (1,0,0)?

$\left(\begin{array}{ccc}{a}_{11}& a_{21}& a_{31}\\ a_{12}& a_{22}& a_{32}\\ a_{13}& a_{23}& a_{33}\end{array}\right)*\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}{a}_{11}*1+a_{21}*0+a_{31}*0\\ a_{21}*1+a_{22}*0+a_{32}*0\\ a_{13}*1+a_{23}*0+a_{33}*0\end{array}\right)=\left(\begin{array}{c}{a}_{11}\\ a_{21}\\ a_{31}\end{array}\right)$

Då kommer vi att få ut en av våra kolumner i avbildningsmatrisen. Mao. om du vet hur basvektorerna avbildas så kan du bilda avbildningsmatrisen.

Skall vi hitta hur som (1,0,0) avbildas längs riktningen (1,1,1) vill det till att vi rör oss med riktningsvektorn t*(1,1,1), där t är vald så att vi stöter på xy-planet. Vår vektor skall alltså avbildas till (1,0,0)+t*(1,1,1)

xy-planet är då z=0, så för att z-värdet i vektorn (1,0,0)+t*(1,1,1) skall bli noll får vi sätta att t blir 0, och att (1,0,0) avbildas på sig själv.

Samma resonemang kan föras på basvektorn (0,1,0).

På (0,0,1) blir det knepigare, för vi skall välja ett t-värde så att (0,0,1)+t*(1,1,1)= ([ett tal],[ett tal],0).

I z-led blir ekvationen att 1+t*1=0 vilket ger

1+t=0

t=-1

så (0,0,1) avbildas på (0,0,1)+(-1)*(1,1,1)= (0-1,0-1,1-1)= (-1,-1,0)

Därmed har vi basvektorernas avbildningar och därmed även A-matrisen.

Jag är osäker på vilken bit i facits resonemang du inte hängde med på, så skriv var du tycker att det fallerar.

Bedinsis skrev:

Ett sätt att se på saken är följande:

Du kommer i slutändan ha avbildningsmatrisen A.

$A=\left(\begin{array}{ccc}{a}_{11}& a_{21}& a_{31}\\ a_{12}& a_{22}& a_{32}\\ a_{13}& a_{23}& a_{33}\end{array}\right)$

Vad händer om man applicerar denna på en av våra basvektorer, t.ex. (1,0,0)?

$\left(\begin{array}{ccc}{a}_{11}& a_{21}& a_{31}\\ a_{12}& a_{22}& a_{32}\\ a_{13}& a_{23}& a_{33}\end{array}\right)*\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}{a}_{11}*1+a_{21}*0+a_{31}*0\\ a_{21}*1+a_{22}*0+a_{32}*0\\ a_{13}*1+a_{23}*0+a_{33}*0\end{array}\right)=\left(\begin{array}{c}{a}_{11}\\ a_{21}\\ a_{31}\end{array}\right)$

Då kommer vi att få ut en av våra kolumner i avbildningsmatrisen. Mao. om du vet hur basvektorerna avbildas så kan du bilda avbildningsmatrisen.

Skall vi hitta hur som (1,0,0) avbildas längs riktningen (1,1,1) vill det till att vi rör oss med riktningsvektorn t*(1,1,1), där t är vald så att vi stöter på xy-planet. Vår vektor skall alltså avbildas till (1,0,0)+t*(1,1,1)

xy-planet är då z=0, så för att z-värdet i vektorn (1,0,0)+t*(1,1,1) skall bli noll får vi sätta att t blir 0, och att (1,0,0) avbildas på sig själv.

Samma resonemang kan föras på basvektorn (0,1,0).

På (0,0,1) blir det knepigare, för vi skall välja ett t-värde så att (0,0,1)+t*(1,1,1)= ([ett tal],[ett tal],0).

I z-led blir ekvationen att 1+t*1=0 vilket ger

1+t=0

t=-1

så (0,0,1) avbildas på (0,0,1)+(-1)*(1,1,1)= (0-1,0-1,1-1)= (-1,-1,0)

Därmed har vi basvektorernas avbildningar och därmed även A-matrisen.

Jag är osäker på vilken bit i facits resonemang du inte hängde med på, så skriv var du tycker att det fallerar.

Riktigt bra förklarat!! Tack för hjälpen, här kommer lösningen jag pysslade ihop: