Trigonometriska identiteter
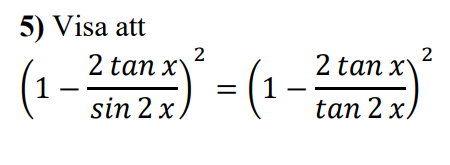Jag löste frågan som följände, undrar om jag har löst den på avancerad nivå? och att jag inkluderade allt som krävs för ett komplett och korrekt svar?
Eftersom både LHS och RHS förenklas till tan^4 (x) innan kvardering, har jag visat att identiteten är sann.
Det är viktigt att betona att processen att förenkla varje sida för att visa att de är lika är det centrala i beviset. Det faktum att båda sidorna förenklas till tan^4 (x) bekräftar att identiteten håller för alla värden på x där uttrycken är definierade.
Instämmer med Yngves svar på din andra tråd. Man riskerar poängavdrag om man inte behandlar definitionsmängderna för VL resp HL.
Ändring av rubrik och kategorisering:
Rubriken har ändrats från "Avancerad fråga!" till "Trigonometriska identiteter".
Att skriva en bra eller lämplig rubrik som beskriver/återspeglar frågan/tråden underlättar betydligt för andra som söker/googlar efter samma fråga.
Tråden har också flyttats från Alla trådar till Trigonometri. /admin
