Att rita en proportionell S-T graf
Jag har svårt att förstå hur värderna på en ST-graf ska infogas/ritas upp på rätt sätt. Den bifogade bilden är ett exempel givet under en föreläsning, och jag kan verkligen inte förstå varför läraren ritat upp den såhär.
De givna (s) värderna enligt tabellen är 0, 15, 22, 27 osv, men läraren har valt att ange sekunderna 0, 10, 20, 30, osv på X-axeln istället. varje "ruta" i X-led innebär därför 2 sekunder, vilket inte är idealt om man vill veta läge (m) efter exakt 15 sekunder. I Y-led däremot, innebär varje "ruta" 50 meter. Varför? Hade det inte varit enklare att ange meter enligt 6:ans multiplikationstabell? alla givna värden i meter följer nämnligen 6ans multiplikationstabell (0, 60, 120 ...), men läraren valde trots detta att skriva Y-led som 0, 50, 100, 150, 200, 250, osv.
Kan man bara "hitta på" grafens exakta angivna värden själv? Måste det inte finnas någon angiven relation mellan Y- och X-led för att grafens "branthet" eller "medelhastiget" ska vara korrekt? Hur ska jag veta med vilka "mellanrum" jag måste distrubera mina X- och Y-värden med?
(Detta är ingen uppgift som måste lösas, utan snarare något som jag personligen uppfattar som oklart/svårt att begripa)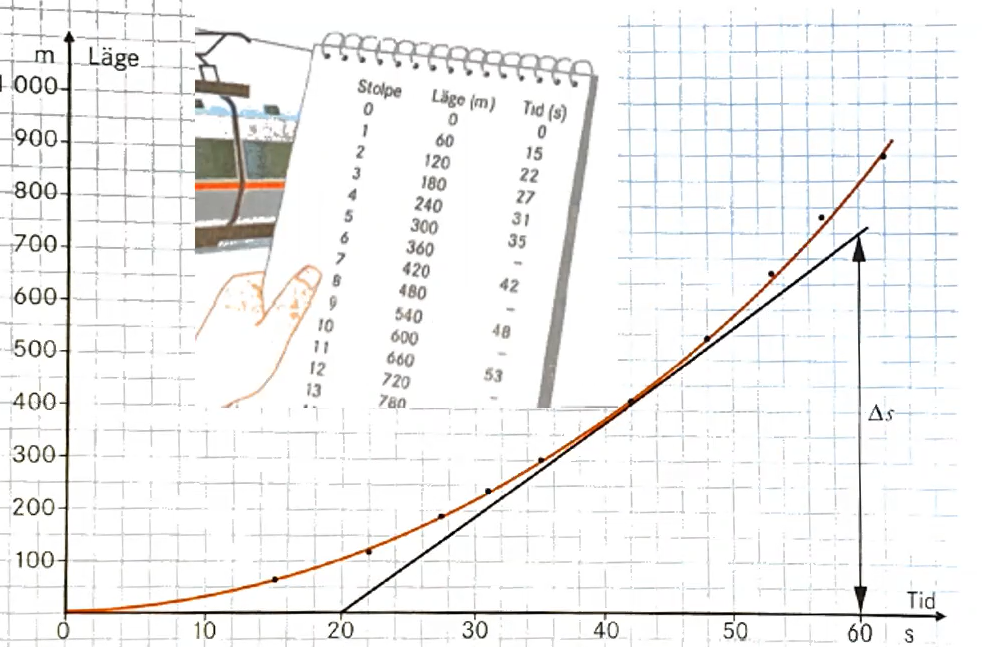
Jag ser inte problemet.
Det är helt enligt konventionerna att ta tid som den oberoende parametern på den horisontella axeln.
Hej och välkommen till pluggakuten! Om jag inte missuppfattar dig så undrar du varför din lärare inte använde en skala på axlarna som gjorde att det var lättare att sätta ut mätpunkterna (men x-axeln var kanske inte så mycket att göra åt...). Det undrar jag också, för naturligtvis ska man göra så, om man inte har fått några speciella instruktioner hur det ska se ut.
Om du funderar på det lite så det enda konsekvens valet av skalor gör, är hur brant kurvan lutar. Om du räknar ut till exempel en momentanhastighet någonstans (tangentens lutning) så blir den densamma oavsett vilka skalor du har valt.
det var exakt detta jag funderade över! Tack så mycket! Använder nästan alltid lärarens exempel som utgångspunkt när jag gör uppgifter, men här hade jag svårt att sätta mig in i lärarens tankesätt.
Och det har du ju helt rätt i, skönt att slippa behöva oroa mig för konsekvenserna av skalan :)
JohanF skrev:Hej och välkommen till pluggakuten! Om jag inte missuppfattar dig så undrar du varför din lärare inte använde en skala på axlarna som gjorde att det var lättare att sätta ut mätpunkterna (men x-axeln var kanske inte så mycket att göra åt...). Det undrar jag också, för naturligtvis ska man göra så, om man inte har fått några speciella instruktioner hur det ska se ut.
Om du funderar på det lite så det enda konsekvens valet av skalor gör, är hur brant kurvan lutar. Om du räknar ut till exempel en momentanhastighet någonstans (tangentens lutning) så blir den densamma oavsett vilka skalor du har valt.



