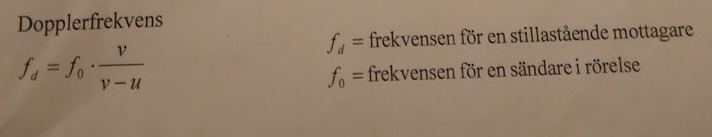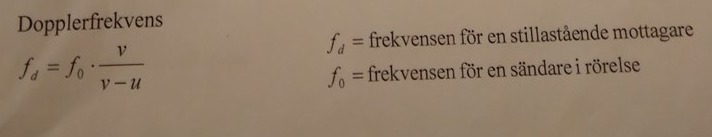Att bestämma en stjärnas radiella hastighet?
Hejsan.
Jag känner mig borttappad med denna uppgift, jag föreställer mig att jag kan använda formeln för rödförskjutning
Med sedan hittar jag bara Hubbles lag v=H0*d, för att beräkna den radiella hastigheten och då jag inte har något d, hur går jag tillväga då?
Skulle verkligen uppskatta tips då frågan tydligen är på E-nivå, vilket då inte skall vara riktigt så svårt.
Frågan:
Vilovåglängderna (dvs. när stjärnan står still) för Balmerseriens linjer är följande:
Hα = 656,272 nm
Hβ = 486,133 nm
Hγ = 434, 047 nm
Hδ = 410,174 nm
Vid en spektralmätning av en stjärna mätte man upp våglängden för Hβ till 486,157 nm.
-
Hur stor är stjärnans radiella hastighet i förhållande till jorden? Med radiell hastighet menas att hastighetens riktning är en förlängning av Jordens radie mot stjärnan. Med andra ord ”rakt mot eller ifrån” Jorden.
-
Var rörelsen riktad mot eller från oss?
Mvh;
Li
Formeln för rödförskjutning verkar bra. Vad får du när du använder den?
Hubbles lag är en empirisk formel för stjärnor på enormt stora avstånd, i alla fall inte inom samma galax. Jag vet inte om den ger nånting här.
Detta är en stjärna i närheten, där Hubbles lag inte gäller.
Här är det bara den vanliga Dopplereffekten.
Laguna skrev:Formeln för rödförskjutning verkar bra. Vad får du när du använder den?
Hubbles lag är en empirisk formel för stjärnor på enormt stora avstånd, i alla fall inte inom samma galax. Jag vet inte om den ger nånting här.
Hejsan och tack för svar, jag behövde bege mig snabbt så jag tog lite tid på mig att svara. Om jag använder formeln för rödförskjutingsfaktorn får jag värdet 49,3668*10^-9.
Jag förstår att jag kan använda formeln för dopplereffekt, men jag förstår den dåligt och mycket förklaringar hittar jag inte heller :)

Pieter Kuiper skrev:Detta är en stjärna i närheten, där Hubbles lag inte gäller.
Här är det bara den vanliga Dopplereffekten.
Hejsan och tack för ditt svar:D
Likt jag sa till Laguna, jag har beräknat rödförskjutningen och förstår att det har med dopplereffekten att göra, men formeln för dopplereffekt förstår jag inte ordentligt och hittar ej heller goda förklaringar till den. Jag hänger med på att f= frekvens v=hastighet u=? och vad står d och 0 för under f?

Linro skrev:Laguna skrev:Formeln för rödförskjutning verkar bra. Vad får du när du använder den?
Hubbles lag är en empirisk formel för stjärnor på enormt stora avstånd, i alla fall inte inom samma galax. Jag vet inte om den ger nånting här.
Hejsan och tack för svar, jag behövde bege mig snabbt så jag tog lite tid på mig att svara. Om jag använder formeln för rödförskjutingsfaktorn får jag värdet 49,3668*10^-9.
Jag förstår att jag kan använda formeln för dopplereffekt, men jag förstår den dåligt och mycket förklaringar hittar jag inte heller :) Jag hänger med på att f= frekvens v=hastighet men u=?
Linro skrev:
Jag hänger med på att f= frekvens v=hastighet u=? och vad står d och 0 för under f?
Det där d-et står säkert för Doppler. Nollan i indexläge är för den ursprungliga frekvensen.
Här hittade du formeln för dopplereffekt av ljud och då är u beteckningen för ljudets hastighet i luft.
I det är fallet behöver du egentligen använda teorin for dopplereffekt av elektromagnetisk strålning i vakuum. Det står säkert i din bok, men se http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/reldop2.html
Pieter Kuiper skrev:Linro skrev:
Jag hänger med på att f= frekvens v=hastighet u=? och vad står d och 0 för under f?
Det där d-et står säkert för Doppler. Subskript 0 är för den ursprungliga frekvensen.
Här hittade du formeln för dopplereffekt av ljud och då är u beteckningen för ljudets hastighet i luft.
I det är fallet behöver du egentligen använda teorin for dopplereffekt av elektromagnetisk strålning i vakuum. Det står säkert i din bok, men se http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/reldop2.html
Tack så mycket för ditt svar, jag fick en uppenbarelse där jag förstod att använda mig av formeln för brytningsindex för ljus n=c/v och sätta lika med formeln för rödförskjutning. Jag förstår hur du menar och är nu på det klara med dopplereffekten. Tack snälla för hjälpen😃