Åt vilket håll ska de 3 sista placeras?
Hej,
Håller på med en uppgift som jag inte riktigt vet hur jag ska lösa på slutet.
Uppgiften är:
Hur många gånger har du motionerat senaste månaden?
11 personer svarande
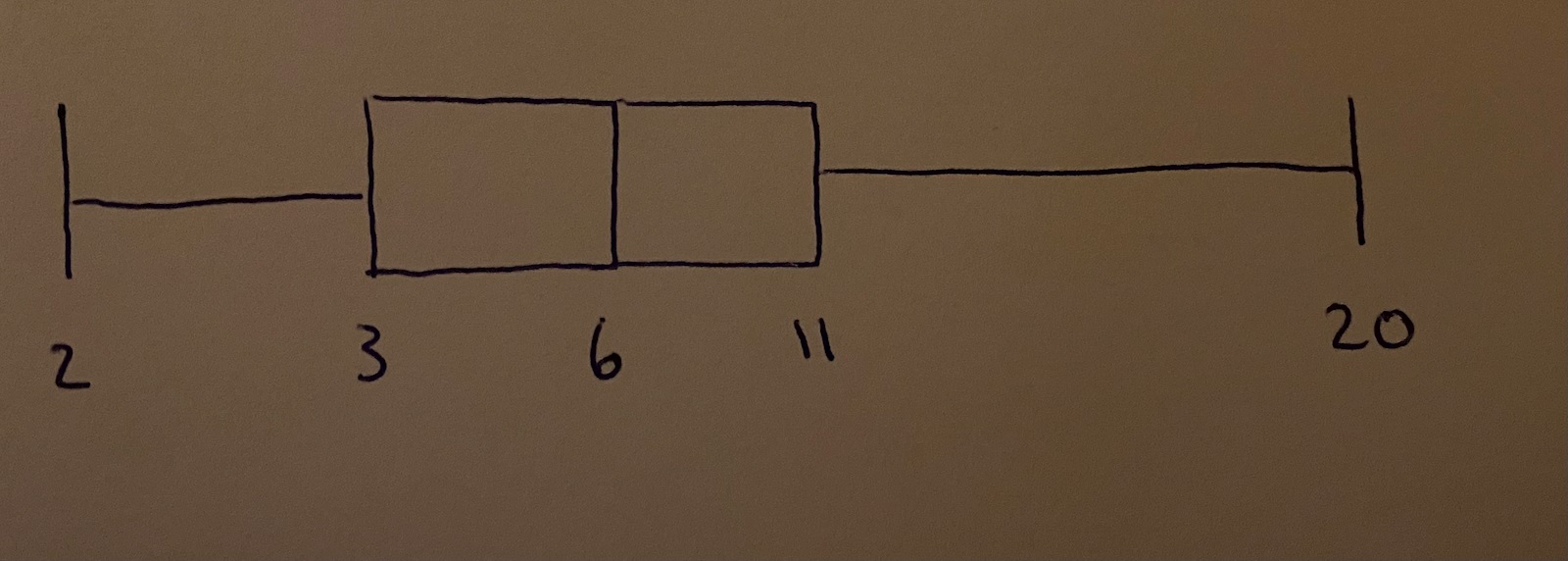
mellan vilka värden kan medelvärdet ligga?
Lösning:
1) 11 personer var med i undersökningen
2)
minst 1 av dom motionera 2g
minst 1 av dom motionera 3g
minst 1 av dom motionera 6g
minst 1 av dom motionera 11g
minst 1 av dom motionera 20g
3) 11-5= 6 personer kvar som man inte vet mycket om.
4) 11 personer är 100%
6 personer kvar att ”fördela ut” på lådagramet
5) 6 är medianen.
6) 6 personer kvar att fördela ut så:
6/2=3
7) 3 personer hör till ”under” medianen som träna mellan 2g-6g
3 personer hör till ”övre” medianen som träna mellan 6-20g
här fastnar jag lite. Jag vet inte vart jag ska placera dessa ”3 övre” & ”3 undre” personerna dvs jag tänker om jag vill veta ett högt medelvärde så kan jag ju placera resten av dessa 3 på 20 respektive 6 så jag får:
2+3+6+6+6+6+11+20+20+20+20/11
och om jag vill ha ett lågt medelvärde så
2+2+2+2+3+6+6+6+6+11+20 /11
och svaret jag får ut är värden mellan, men vet inte om jag kan tänka så riktigt.
jag har ju redan den nedre kvartil & övre kvartil så jag vet ju att 3:an är medianen av de 3 så betyder de då att 2 av de tre ska vara mellan 2&3 & 1 ska vara mellan 3-6 och om 11 är medianen för de övre & jag har 3 kvar så är de då 2 kvar mellan 11-20 och 1 mellan 6-11 eller tvärtom? Alltså åt vilket håll ska de 3 sista delas upp och placeras?
**
Jag har försökt se på bilden om jag kanske kan få någon info där, men liksom inte så mycket egentligen, vet bara att de är en hög spridning mellan 11 och 20 typ och en längre spridning mellan 2 och 3, så blir osäker på hur jag ska tänka/göra?
***
Sorry lägger till här igen:
Tror de skulle bli enklare att veta om jag kan räkna fram den nedre kvartilen samt den övre kvartilen själv.
Blir något osäker på hur dom får fram 3 samt 11 men!
På 3: tänker jag:
om 6 är medianen så har jag ju: 2,3,4,5, innan 6.
Om 6 är medianen (och försvinner/inte räknas med) har jag 2,3,4,5 kvar
Medianen blir ju då 3,5 och inte 3. . . .
Men om jag skulle räkna med 1 dvs 1,2,3,4,5 DÅ får jag 3 som median!
På 11: tänker jag:
Om 11 är medianen mellan 7 och 20... då fattar jag faktiskt inte hur dom tänker..
hm..
Jag har 11 personer
11-3 = 8
8/2 =4
4 tillhör medianen UNDER 6
4 tillhör medianen ÖVER 6
Medianen under 6 får 4 personer till sig (med 2:an som redan finns där så är det 5 totalt)
x, 2, x, x, x, 6
Medianen blir då den i parentes:
x, 2, (x), x, x,
dvs 3 !
om jag gör samma ÖVER medianen 6 så:
6, x, x, x, x. (6,7,8,9,10)
Förstår jag inte hur dom fått fram 11 ?
Förslag på resonemsng:
Det är 11 observationer. Vi kan kalla dem osv upp till , där osv.
Är du med på att vi kan avläsa följande ur lådagrammet?
Återstår att välja värden på , där vi begränsas av
Om vi nu vill att medelärdet ska var så högt/lågt som möjligt så ska vi välja dessa värden vara så stora/små som möjligt.
Kommer du vidare då?
Tack för svaret. okej, jag hänger typ med.
Men undrar hur du kommer fram till att: x3+x4/2=3 ? och x8+x9/2=11 ?
Har läst ditt svar och tänker, okej! Om:
x1=2
x6=6
x11=20
dvs 3 av dessa 11 personer är "upptagna" så jag har 8 personer kvar. Det förstår jag.
om man då har:
11 deltagare (x1,x2,x3,x4 osv)
x1 =2 (dvs har tränat 2g) "första personen"
x2
x3 = dessa blir mitt i mellan 1 och 6 så addera ihop sedan /2
& då får man fram nedre kvartil ?? hur blir det 3??
x4 = dessa blir mitt i mitten 1 och 6 så addera ihop sedan /2
x5
x6 =6 (dvs har tränat 6g)
x7
x8 = dessa blir mitt i mitten 6 och 11 så addera ihop sedan /2
& då får man fram övre kvartil ?? Hur blir det 11??
x9 = dessa blir mitt i mitten 6 och 11 så addera ihop sedan /2
x10
x11 = (dvs har tränat 20g) "sista personen"
Jag har då:
x2 kvar. x2 ligger mellan 2 och 3 ?
x5 kvar. x5 ligger mellan 3 och 6 ?
x7 kvar. x7 ligger mellan 6 och 11 ?
x10 kvar. 10x ligger mellan 11 och 20 ?
Jag har då, 11 personer. Vissa av dessa 11 vet man hur de tränat och några vet man inte.
De personer man vet har tränat X antal gånger i månaden har sitt "fasta" antal, de andra är "rörliga"
Vill jag ha ett högt medelvärde så placerar jag dessa närmare den högre siffran/gångerna som de tränats
Vill jag ha ett lägre medelvärde så placerar jag dessa närmare den lägre siffran/gångerna som de tränats
Så då blir de väl: (om jag utgår från att 3 är nedre kvartil och 11 är högre kvartil)
x1 första personen = Tränat 2 gånger
x2 andra personen= Tränat ANTINGEN Låg gång: 2g Hög gång: 3g
x3 tredje personen= Tränat 3gånger
x4 fjärde personen= Tränat ANTINGEN låg gång: 3g Hög gång: 6g
x5 femte personen= Tränat ANTINGEN låg gång: 3g Hög gång: 6g
x6 sjätte personen= Tränat 6 gånger
x7 sjunde personen= Tränat ANTINGEN låg gång: 6g Hög gång: 11 g
x8 åttonde personen= Tränat ANTINGEN låg gång: 6g Hög gång 11g
här mellan är högre kvartil
x9 nionde personen= Tränat ANTINGEN låg gång: 11g Hög gång 20g
x10 tionde personen= Tränat ANTINGEN låg gång: 11g Hög gång 20g
x11 Elfte personen = Tränat 11 gånger
Räknar fram medelvärdet och mellan dessa Hög och Låg där mellan är svaret på uppgifte?
Naturens skrev:Tack för svaret. okej, jag hänger typ med.
Men undrar hur du kommer fram till att: x3+x4/2=3 ? och x8+x9/2=11 ?
Nej, fel av mig. Det gäller att nedre kvartilen är det tredje vördet, dvs x3 och den övre kvartilen är det nionde värdet, dvs x9.
Det ger oss att x3=3 och att x9=11.
Värdena är alltså 2, x2, 3, x4, x5, 6, x7, x8, 11, x10 och 20.
Sedan tidigare vet vi att
Okej, men jag förstår inte det här:
"Det gäller att nedre kvartilen är det tredje vördet, dvs x3 och den övre kvartilen är det nionde värdet, dvs x9."
Hur vet du det?hur tänker du fram det? Låt säga om man inte visste att nedre kvartilen är 3 och övre kvartilen är 11, hur får man fram det genom att se ett lådagram som har värderna:
Lägsta värde 2
Högsta värde 20
median 6
Jag tänker ju då att:
1
2
3. - detta blir nedre kvartilen
4
5
6 - median räknar ej med antar jag? (hur vet man när man ska rärkna med denna?)
7 *
8 *
9*
10*
11*
12*
13
14+13= 27, 27/2 = 13,5 ? de blir ju inte 11 ens här ?
14
15*
16*
17 *
18 *
19 *
20 *
Naturens skrev:Okej, men jag förstår inte det här:
"Det gäller att nedre kvartilen är det tredje vördet, dvs x3 och den övre kvartilen är det nionde värdet, dvs x9."
Hur vet du det?hur tänker du fram det? Låt säga om man inte visste att nedre kvartilen är 3 och övre kvartilen är 11, hur får man fram det genom att se ett lådagram som har värderna:
Lägsta värde 2
Högsta värde 20
median 6
Jag tänker ju då att:
1
2
3. - detta blir nedre kvartilen
4
5
6 - median räknar ej med antar jag? (hur vet man när man ska rärkna med denna?)
7 *
8 *
9*
10*
11*
12*
13
14+13= 27, 27/2 = 13,5 ? de blir ju inte 11 ens här ?
14
15*
16*
17 *
18 *
19 *
20 *
Läs t.ex. här om vad kvartiler är och hur man bestämmer dem.
okej men det är väl så jag tänker ju?... om:
"3:e värdet den första kvartilen, det 6:e värdet andra kvartilen och det 9:e värdet den 3:e kvartilen. av 11"
11 deltagare:
x1
x2
x3 = 3:e värdet blir: Första kvartil/ lägre kvartil. Värde 3
x4
x5
x6 = 6:e värdet blir: median /andra kvartil Värde 6
x7
x8
x9 = 9:e värdet blir: Tredje kvartil / högsta kvartil Värde blir då: 9
x10
x11
Jag vet att jag vid 9:e värdet kan "luta" den högsta kvartilen mot antingen 11 (för att få lågt medelvärde) och då blir de 9:e värdet 11, eller luta det 9:e värdet mot 20 för att då få det 9:e värdet till 20 dvs räkna de som 20 och få ett högt medelvärde. Men fortfarande så är de ju 9 OM jag utgår från 11.
om det istället är 20 då blir de ju andra värden blir de inte? det känns som jag missar något... =/
***
blir osäker nu på om jag tänker rätt när de kommer till det här med kvartiler, har ju fått rätt på andra uppgifter om sånt!
Naturens skrev:okej men det är väl så jag tänker ju?... om:
"3:e värdet den första kvartilen, det 6:e värdet andra kvartilen och det 9:e värdet den 3:e kvartilen. av 11"
I svar #5 skrev du 20 rader numrerade 1-20, (vissa med en stjärna efter numret av okänd anledning). Du skrev att (14+13)/2 = 13,5 som inte är lika med 11. Det tolkade jag som att du inte riktigt hade koll på att antalet observationer är 11, inte 20.
Därför länkade jag till en sida som beskriver vilka kvartilerna är om antalet observationer är 11.
11 deltagare:
x1
x2
x3 = 3:e värdet blir: Första kvartil/ lägre kvartil. Värde 3
x4
x5
x6 = 6:e värdet blir: median /andra kvartil Värde 6
x7
x8
x9 = 9:e värdet blir: Tredje kvartil / högsta kvartil Värde blir då: 9
x10
x11
Nej, detta stämmer inte. Enligt lådagrammet i ursprungsinlägget så är x1 = 2, x3 = 3, x6 = 6. x9 = 11 och x11 = 20.
Jag vet att jag vid 9:e värdet kan "luta" den högsta kvartilen mot antingen 11 (för att få lågt medelvärde) och då blir de 9:e värdet 11, eller luta det 9:e värdet mot 20 för att då få det 9:e värdet till 20 dvs räkna de som 20 och få ett högt medelvärde. Men fortfarande så är de ju 9 OM jag utgår från 11.
Nej, det 9:e värdet är 11, det går inte att ändra på. Däremot kan det 10:e värdet vara vad som helst från och med 11 till och med 20.
om det istället är 20 då blir de ju andra värden blir de inte? det känns som jag missar något... =/
Ja, du missar att x1, x3, x6, x9 och x11 är bestämda.
***
blir osäker nu på om jag tänker rätt när de kommer till det här med kvartiler, har ju fått rätt på andra uppgifter om sånt!
Svaret på denna uppgift:
- För att få ett så lågt medelvärde som möjligt så skall de värden som inte redan är bestämda vara så låga som möjligt. Vi får då att de 11 värdena ska vara 2, 2, 3, 3, 3, 6, 6, 6, 11, 11, 20, där de fetmarkerat indikerar de bestämda värdena.
- För att få ett så högt medelvärde som möjligt så skall de värden som inte redan är bestämda vara så höga som möjligt. Vi får då att de 11 värdena ska vara 2, 3, 3, 6, 6, 6, 11, 11, 11, 20, 20, där de fetmarkerat indikerar de bestämda värdena.
Tack. Jag vet vart jag tänkte fel nu. Fastna vid att Person 9 INTE behöver ha 9 som värde utan det är ju faktiskt 11 som uppgiften visar och som du skrev! Det var där jag bara liksom, ja, inte kunde ta mig själv vidare från! Hur som tack!
Behöver nog göra fler såna här uppgifter för att förstå tänket bättre!


