asympt.
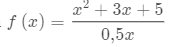
Hur bestämmer jag asymptoter för denna funktion smidigt?
Hej.
Eventuella vertikala asymptoter hittar du vid de x-värden där funktionsvärdet går mot plus eller minus oändligheten.
Eventuella horisontella asymptoter hittar du om funktionsvärdet går mot ett konstant värde då x går mot plus eller minus oändligheten.
Eventuella sneda asymptoter kan du hitta genom att följa denna beskrivning.
Yngve skrev:Hej.
Eventuella vertikala asymptoter hittar du vid de x-värden där funktionsvärdet går mot plus eller minus oändligheten.
Eventuella horisontella asymptoter hittar du om funktionsvärdet går mot ett konstant värde då x går mot plus eller minus oändligheten.
Eventuella sneda asymptoter kan du hitta genom att följa denna beskrivning.
Är x2 en asymptot, för att det är den som dominerar när man sätter in stora tal?
Om en funktion f(x) kan skrivas som f(x) = kx + m + r(x), där r(x) är en funktion som går mot noll då x går mot positiva eller negativa oändligheten så säger vi att linjen y = kx + m är en asymptot till f(x) då x går mot positiva (eller negativa) oändligheten.
I vårt fall så gäller det att
f(x) = = .
Vi ser att y = 2x + 6 är en asymptot då x går mot positiva (eller negativa) oändligheten, eftersom som 10/x går mot noll då x går mot positiva (eller negativa) oändligheten. Vi kan således se 10/x som r(x) i detta fall.




