Fusion av helium till kol
Har denna fråga jag försökt att lösa :
Min lösning var
Tänker/gör jag rätt är det rimligt ?


b-uppgiften.
Vad är massan för en alfapartikel?
Varför blandar du in ljushastigheten när du beräknar energin med hjälp av omvandlingsfaktorn 931.5 MeV/u?
Vad är massan för en alfapartikel?
Massan av en alfapartikel är :
6,644 657 × 10 −27 kg
Ska jag bara ta bort ljushastigheten och beräkningen blir rätt ? Hur ska jag göra , formel elr så ?
Sara.alaga._12345 skrev:
Vad är massan för en alfapartikel?
Massan av en alfapartikel är :
6,644 657 × 10 −27 kg
Ska jag bara ta bort ljushastigheten och beräkningen blir rätt ? Hur ska jag göra , formel elr så ?
Jag tror att du har slarvat lite bara, men jag vet inte riktigt hur, för dina (felaktiga) insatta värden stämmer inte heller med dina svar.
Alfapartikel är samma sak som en heliumkärna, betecknas H4e och består av två neutroner och två protoner. Dvs den borde väga kring 4u (jag har ingen tabellsamling, så du måste slå upp det exakta värdet själv).
Jag förstår inte riktigt hur du lyckas beräkna massdefekten med den felaktiga alfapartikelmassan.
När du beräknar energin, så använder du mass-till-energi-omvandlingsfaktorn 931.5 Mev/u i dina beräkningar. Den finns säkert i din formelsamling, och är bekväm att använda, men om du använder den omvandlingsfaktorn så kan du inte också multiplicera med kvadraten av ljushastigheten.
Kan du se över dina beräkningar ännu en gång, för du verkar vara på rätt väg.
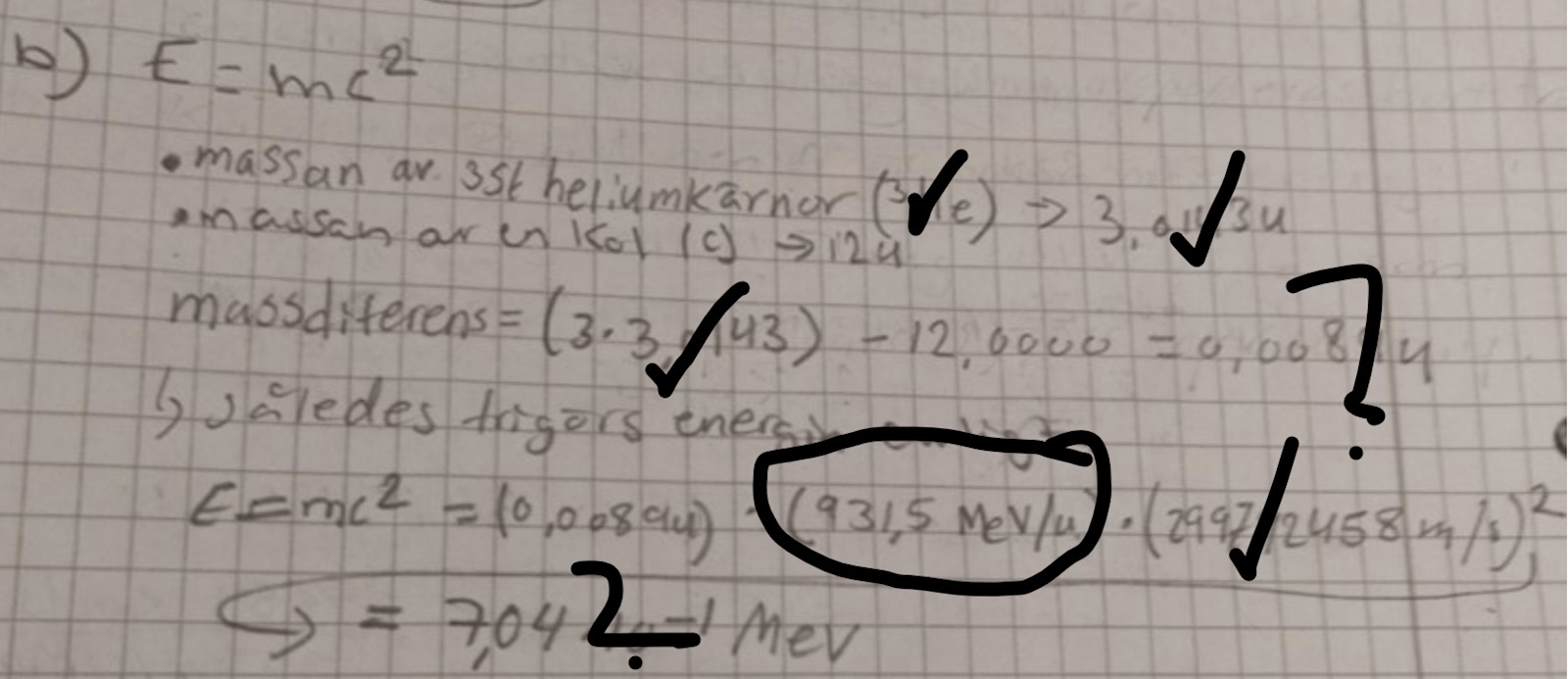
E = mc2
* Massan av en alalfapartikel = 3.016029 (He) × 4 = 12,064116 u
* Massan av en kol (c) = 11,011434 u
Massdiferensen = 12,064116 u - 11,011434 = 1,052682 u
→ således frigörs energin enligt :
E=mc2 = 1,052682 u * ( 931,5 MeV/u )2 =
913 404,013 MeV
~ såhär blir det med exakta siffror och om jag skriver om .är det så du vill säga ?
Sara.alaga._12345 skrev:E = mc2
* Massan av en alalfapartikel = 3.016029 (He) × 4 = 12,064116 u
* Massan av en kol (c) = 11,011434 u
Massdiferensen = 12,064116 u - 11,011434 = 1,052682 u
→ således frigörs energin enligt :
E=mc2 = 1,052682 u * ( 931,5 MeV/u )2 =
913 404,013 MeV
~ såhär blir det med exakta siffror och om jag skriver om .är det så du vill säga ?
Ja, jag tror resonemanget stämmer om man sätter in korrekta siffror och räknar rätt.
Men jag förstår fortfarande inte dina siffror för massdifferensen. Tyvärr har jag ingen formelsamling så jag kan kontrollera. Var hittar du värdet för heliumkärnans He-4 massa? Du skriver 3.016029u, men jag tycker att det borde vara någonstans kring 4u. Kan du klippa in en bild på tabellen i din formelsamling, så vi kan kontrollera?
Samma sak med C-12, var hittar du uppgiften 11.011434u? Klipp en bild på din formelsamling så kontrollerar vi.
Nu kvadrerar du plötsligt omvandlingsfaktorn 931.5MeV/u. Varför gör du det? Det gjorde du inte förut.
Kan du snälla skriva mig vad du menar tydligt..tänkte du sa att jag bör it använda ljushastigheten ...hur ska jag göra , har fastnat i denna upgift nu (?) .
Men det är rätt formler va äre som blir fel i så fall ?
Sara.alaga._12345 skrev:E = mc2
* Massan av en alalfapartikel = 3.016029 (He) × 4 = 12,064116 u
* Massan av en kol (c) = 11,011434 u
En alfapartikel är ungefär 4u, använd nuklidmassa för He42.
Det uppstår kol-12 i trippel-alfaprocessen, alltså utav tre stycken helium.
Nuklidmassa av kol-12 är 12u (enligt en definition).
Använd detta för att beräkna masskillnaden.
Sara.alaga._12345 skrev:Kan du snälla skriva mig vad du menar tydligt..tänkte du sa att jag bör it använda ljushastigheten ...hur ska jag gör har fastnat i denna upgift nu :/
Förlåt, jag tyckte att du var så nära från början, så jag ville inte hjälpa dig för mycket på direkten.
När man räknar på massdefekten så är det jätteviktigt att använda så bra värden som man kan (dvs tabellvärden med många decimaler), annars blir det stora fel i resultatet. Därfär jätteviktigt att läsa av nukleidmassan för He-4 och C-12, och ingenting annat. Du skrev ju dessa isotoper i reaktionsformeln på a-uppgiften, sen så använde du något annat i b-uppgiften.
Massdefekten=3*4.002603-12.00000=0.007809u
När man omvandlar massan till energi så kan man helt enkelt använda genvägen med omvandlingsfaktorn 931.5MeV/u, eftersom den finns i din formelsamling.
ELLER så kan man räkna E=mc2, vilket såklart är samma sak, men du måste då omvandla till SI-enheter. Du kan INTE använda en blandning av dessa beräkningsmetoder.
Så antingen:
E=0.007809u*931.5MeV/u=7.3MeV
Eller:
E=mc2=0.007809u
Vilket är lika stor energi, men mätt i SI-enheten Joule istället för enheten MeV.
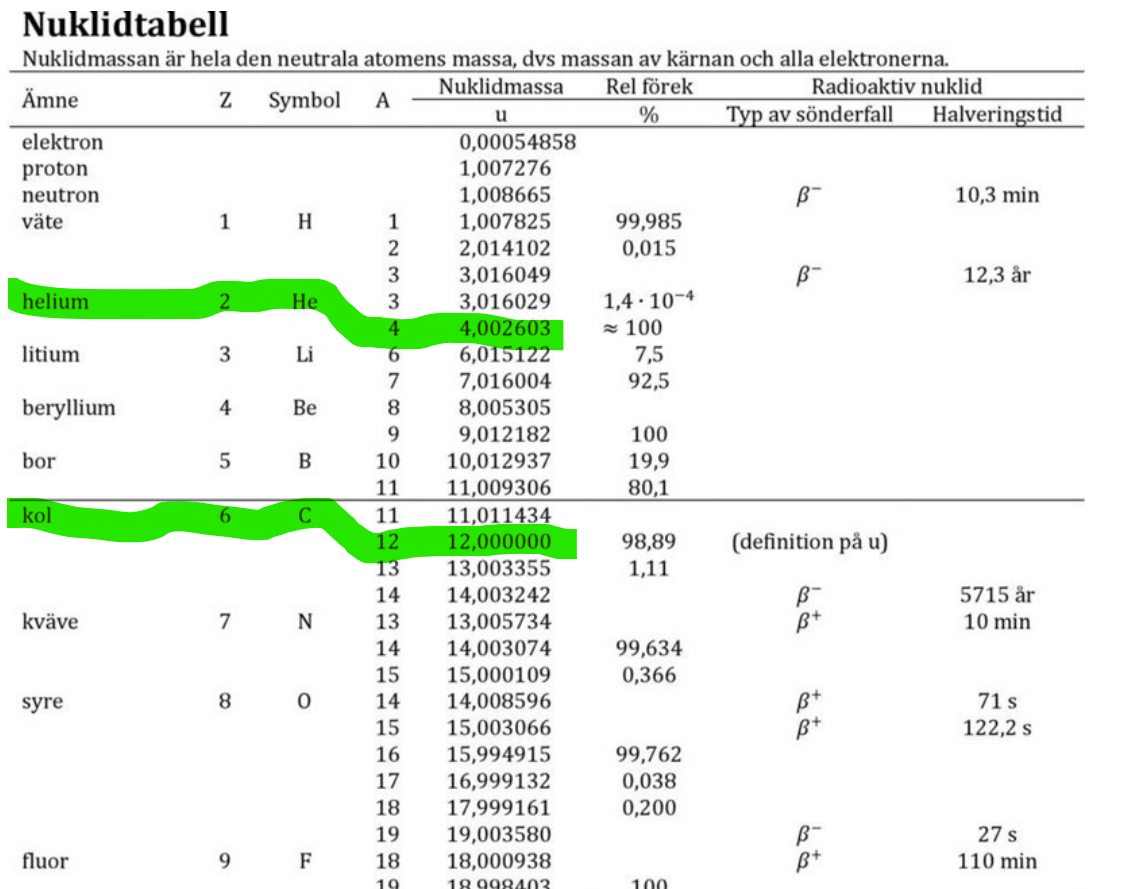
Nedan har jag markerat hur du måste avläsa tabellen för isotopmassor. Om du av misstag råkar läsa av massorna för He-3 eller C-11, så kommer du att få negativa värden på massdefekten (eller nåt annat orealistiskt) och det blir pannkaka av hela uppgiften.
Tack för hjälpen,nu förstår jag ! :)




