Aritmetik - trick med 3 siffror
Hej!
Har en fråga där jag ska bevisa följande "taltrix":
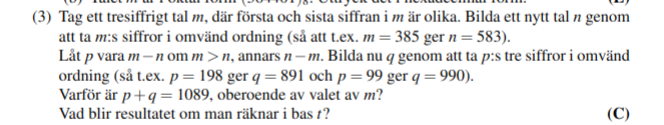
Facit säger följande:
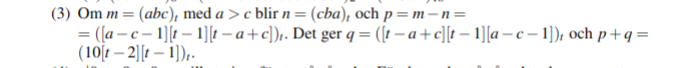Jag känner mig dåligt inläst på den bakomliggande principen bakom additionsuppställning. Om vi "ställer upp" m.h.a. additionsuppställning ser vi ju att i mittensiffran har vi en "carry over" till den mest signifikanta siffran, oberoende bas. Men är den carry overn alltid 10 oavsett bas? Jag förstår med andra ord inte varför facit har just en 10 på följande plats:
.
Jag fick by the way fram formeln att talet i bas ges av
. Är det fel att svara med en formel istället?
Mange takk!
10 betecknar talet 10^1 i bas 10, men t.ex. 8^1 i bas 8, eller t^1 i bas t.
Det är inte fel att svara med en formel så länge man visat att det blir 1089 för t = 10 och att den inte beror på m.
10 betecknar talet 10^1 i bas 10, men t.ex. 8^1 i bas 8, eller t^1 i bas t.
Så borde det då stå
i facit eller tänker jag fel?
Nja, t är inte en siffra i bas t utan det blir siffran 1 följt av siffran 0. Kanske hade man kunnat skriva [1][0][t-2][t-1] för tydlighetens skull. Har inte sett någon liknande notation förut.
