Areor mellan kurvor - integraler

Hej jag behöver hjälp med att försöka förstå mig denna uppgift. När jag försökte lösa denna uppgift började med att hitta lutningen på den räta linjen. Detta gjorde jag genom att ta ( $(1 - 0) / (0 - (p i / 2))$ vilket blir (-2/pi) Som ni ser i facit så stämmer detta inte överens. En till sak som jag inte förstår mig på är att lutningskoefficienten är själv och inte multiplicerat med ett x, borde inte den primitiva funktionen då bli 0?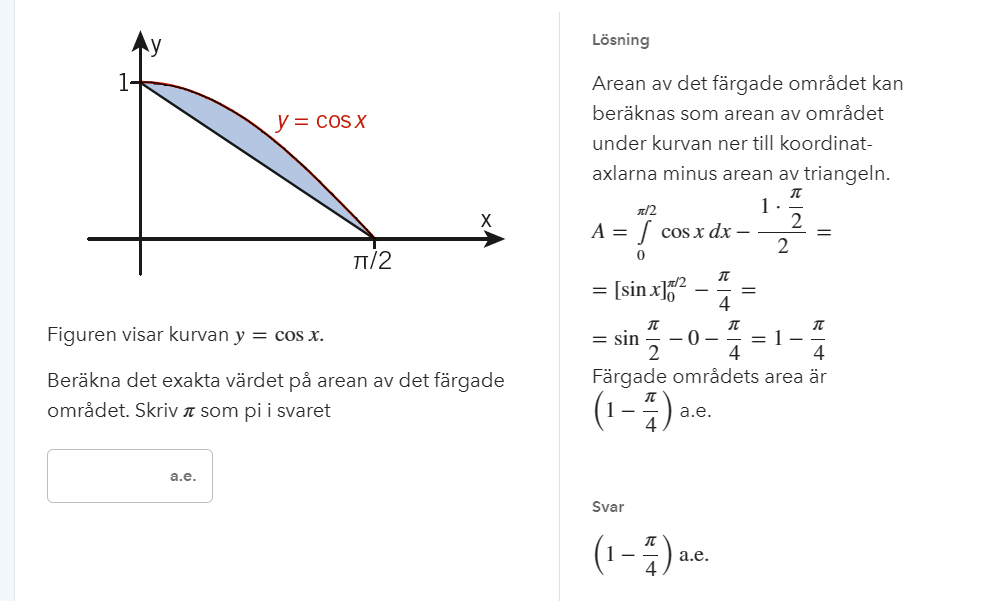

Hej!

Linjen som du får blir $y = - \frac{2}{π} x + 1$ . Integrerar du den får du

$\int_{0}^{π / 2} - \frac{2}{π} x + 1 d x = {[- \frac{x^{2}}{π} + x]}_{0}^{π / 2} = - \frac{1}{π} (\frac{π^{2}}{4}) + (\frac{π}{2}) - (- \frac{1}{π} {(0)}^{2} + 0) = \frac{π}{4}$

Men de löser det geometriskt, genom att beräkna arean av triangeln under $y = - \frac{2}{π} x + 1$ , alltså

$\frac{(b \times h)}{2} = \frac{1 \times \frac{π}{2}}{2} = \frac{π}{4}$

De beräknar sedan arean under $\cos (x)$ och tar bort arean av triangeln.

Sen för att kommentera "En till sak som jag inte förstår mig på är att lutningskoefficienten är själv och inte multiplicerat med ett x, borde inte den primitiva funktionen då bli 0?"

Nej, integralen av en konstant $α$ blir $α x + β$ , och tänker vi geometriskt igen så är en konstant funktion endast ett rakt streck, det blir alltså som att beräkna arean av en rektangel! (testa detta i t.ex. geogebra eller desmos om du inte förstår) Så enda gången integralen av en konstant blir 0 är om konstanten är 0.

Hoppas jag gjorde dina funderingar lite klarare!

Svara