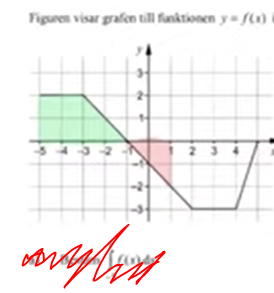
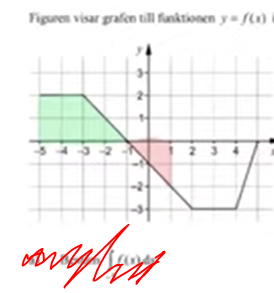
arean vid integrering
har inte riktigt förstått hur jag vet vart gränsen vid y-värdet går vid en integrering
exempel:
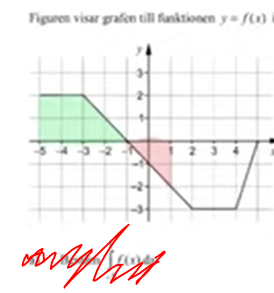
hur vet jag att det exempelvis bara är det gröna området är där integreringen går och inte mer ner? och hur visste man att det var just det rosa?
likaväl här
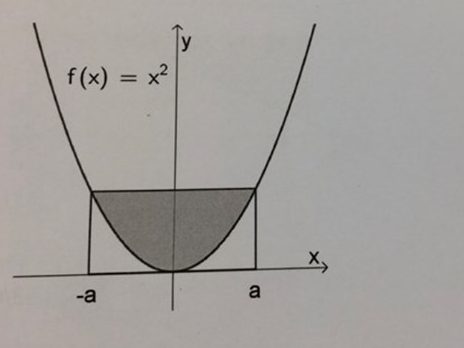
tydligen ger integreringen av -a och a arean av det vita området, om jag förstått rätt? bör inte det vara den gråa arean? hur vet man att den inte täcker mer?
naturnatur1 skrev:har inte riktigt förstått hur jag vet vart gränsen vid y-värdet går vid en integrering
exempel:
hur vet jag att det exempelvis bara är det gröna området är där integreringen går och inte mer ner? och hur visste man att det var just det rosa?
Man integrerar inom ett intervall.
För integreringar så gäller att ”arean” som räknas ut är mellan de grafer som väljs.
Om du har två funktioner f(x) och g(x) så är arean mellan de i ett visst intervall:
integralen(f(x)-g(x))
Nu i början så räknar du bara på arean mellan given funktion och x-axeln. Därför det blir som det på de exemplena du skickade.
Varför det blir just arean mellan exempelvis funktion f(x) och x-axeln när man tar:
integralen(f(x))
beror på att man kan se x-axeln som en funktion enligt g(x)=0 dvs
integralen(f(x)-g(x)) = integralen(f(x)-0) = integralen(f(x))
Hänger du med lite iaf eller var jag jätteflummig?😅
mrpotatohead skrev:naturnatur1 skrev:har inte riktigt förstått hur jag vet vart gränsen vid y-värdet går vid en integrering
exempel:
hur vet jag att det exempelvis bara är det gröna området är där integreringen går och inte mer ner? och hur visste man att det var just det rosa?
Man integrerar inom ett intervall.
För integreringar så gäller att ”arean” som räknas ut är mellan de grafer som väljs.
Om du har två funktioner f(x) och g(x) så är arean mellan de i ett visst intervall:
integralen(f(x)-g(x))
Nu i början så räknar du bara på arean mellan given funktion och x-axeln. Därför det blir som det på de exemplena du skickade.
Varför det blir just arean mellan exempelvis funktion f(x) och x-axeln när man tar:
integralen(f(x))
beror på att man kan se x-axeln som en funktion enligt g(x)=0 dvs
integralen(f(x)-g(x)) = integralen(f(x)-0) = integralen(f(x))
Hänger du med lite iaf eller var jag jätteflummig?😅
jo lite(:
man räknar alltså mellan given funktion och x-axeln, men förstår dock fortfarande inte hur det blir att man räknar fram det vita området, och inte det gråa?
Integrering ger arean under kurvan.
Vill man ha en djupare förståelse får man bryta ner det till Riemannsummor