Arean delas i två lika delar
Arean i första kvadranten som innesluts av positiva x-axeln, linjen samt funktionen:
delas i två lika stora delar av en rät linje med negativ lutning som går genom punkten . Bestäm skärningspunkten mellan denna linje och kurvan .
Jag får x = 0.362194. Inte speciellt snyggt. Är uppgiften rätt avskriven?
Helt rätt Trinity2! Den är ej avskriven eftersom jag hittade på den själv. Håller dock med om att jag kunde valt funktionen så att det blev en snyggare och jämnare lösning som ett exakt uttryck.
Kan tjäna som en bra "kombinationsuppgift" för gymnasiet. Integral + NR.
Troligen även en bra uppgift för grafräknare.
Håller med. Hur löste du den? Är ju lite lurig eftersom integrationsgränserna beror av linjens lutning.
tomast80 skrev:Håller med. Hur löste du den? Är ju lite lurig eftersom integrationsgränserna beror av linjens lutning.
Låt F(x) vara primitiv funktion till f(x) och x=a det värde vi söker.
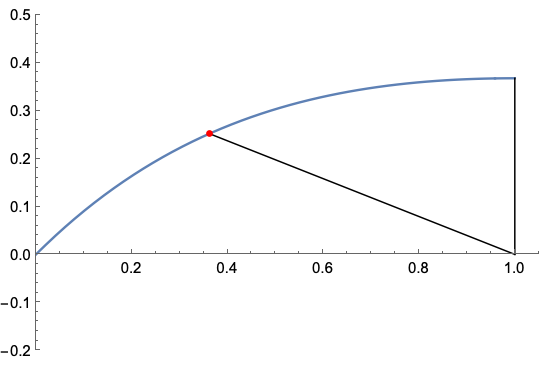
Drag en lodrät linje x=a i ovanstående figur som träffar den röda punkten.
Detta ger upphov till 3 areor, A1, A2 och A3 där A2 är en triangel.
Vi har ekvationen
A1 + A2 = A3
Men A1 = INT_0^a och A3 = INT_a^1 - A2 så
INT_0^a + A2 = INT_a^1 - A2
2*A2 = INT_a^1 - INT_0^a
Då
2*A2 = 2 * 1/2 * (1-a)f(a) = (1-a)f(a)
och
INT_a^1 - INT_0^a = F(1)-F(a)-(F(a)-F(0)) = F(0)+F(1)-2F(a)
har vi att
(1-a)f(a) = F(0)+F(1)-2F(a).
Sätt
g(a) = (1-a)f(a) - ( F(0)+F(1)-2F(a) )
och lös g(a)=0 med NR. Jag tror inte den är analytiskt lösbar.
a ≈ f(1) = 1/e, men det är en tillfällighet.
Elegant lösning, Trinity2!


