Arean av en fyrhörning med diagonaler vinkelräta mot varandra

Tänkte att man skulle kunna räkna som en romb, diagonal x diagonal_2/2 eftersom den har räta vinklar. Men det är bara vad min intuition sa
Ja, det fungerar bra. Om du känner dig osäker, prova att rita! :)
Smutstvätt skrev:Ja, det fungerar bra. Om du känner dig osäker, prova att rita! :)
Har provat att rita och kan inte motivera hur jag ska lösa denna
henrikus skrev:
juste det finns någon sats som säger typ y*x=z*w eller något sånt va
Ja, kanske, men det är nog bara att beräkna arean som en summa av trianglars area så ska det nog ordna sig.
henrikus skrev:Ja, kanske, men det är nog bara att beräkna arean som en summa av trianglars area så ska det nog ordna sig.
ok A_1=(5-x)(4)/2
A_2=(5-y)(4)/2
Kommer inte längre än så
En romb med höjden fem och bredden fyra:
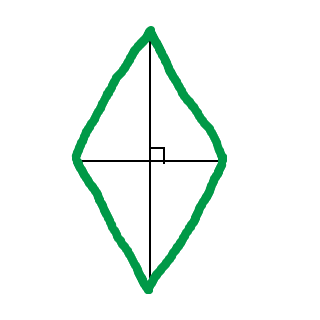
Eftersom diagonalerna är vinkelräta har vi fyra lika stora trianglar => 4 * trianglarnas area, alternativt hälften av arean av en rektangel med samma mått. :)
A=(xw+xz+yw+yz)/2=(x(w+z)+y(w+z))/2=(x+y)(w+z)/2=5*4/2=10
henrikus skrev:A=(xw+xz+yw+yz)/2=(x(w+z)+y(w+z))/2=(x+y)(w+z)/2=5*4/2=10
ajajaj, snyggt!! :))
Det behöver dock inte vara en romb.
Diagonalerna är ju vinkelräta dock?
Smutstvätt skrev:Diagonalerna är ju vinkelräta dock?
Om du menar att det borde vara en romb därför, så stämmer det inte alltid testa att låta ena diagonalen skära den andra i botten av den andra
Aha, ja jo det är sant. Det specialfallet tänkte jag inte på. 😅





