Arean av det färgade området uttryckt i a och b.

Hej.

Tips: Försök att hitta tre rätvinkliga  trianglar i bilden.

Skriv uttryck för trianglarnas area A₁, A₂ och A₃.

Kommer du vidare då?

Jag har försökt rita en vinkel rät linje genom A och CB

Du behöver inte rita något.

Är du med på att

• ABC är en rätvinklig triangel med area AB•AC/2, vilket är lika med b²/2?
• ADC är en rätvinklig triangel med area AD•AC/2, vilket är lika med ab/2?
• ABE är en rätvinklig triangel med area AB•AE/2, vilket är lika med ab/2?

Arup har inte hört av sig mer.
Yngve, jag är nyfiken på din metod. Jag tyckte problemet var intressant, så jag har jobbat fram flera olika mer eller mindre krångliga metoder (en ganska enkel). Men du verkar ha siktat på något annat och enkelt som jag inte kan se.

Louis skrev:

Arup har inte hört av sig mer.
Yngve, jag är nyfiken på din metod. Jag tyckte problemet var intressant, så jag har jobbat fram flera olika mer eller mindre krångliga metoder (en ganska enkel). Men du verkar ha siktat på något annat och enkelt som jag inte kan se.

Nej, jag inser nu att jag tänkte helt fel.

Man kan kalla skärningspunkten (x,x) och använda det för att skära av en topptriangel från den vänstra rätvinkliga triangeln Yngve menar.  Då får vi ett värde på x och sedan är vi nästan hemma.

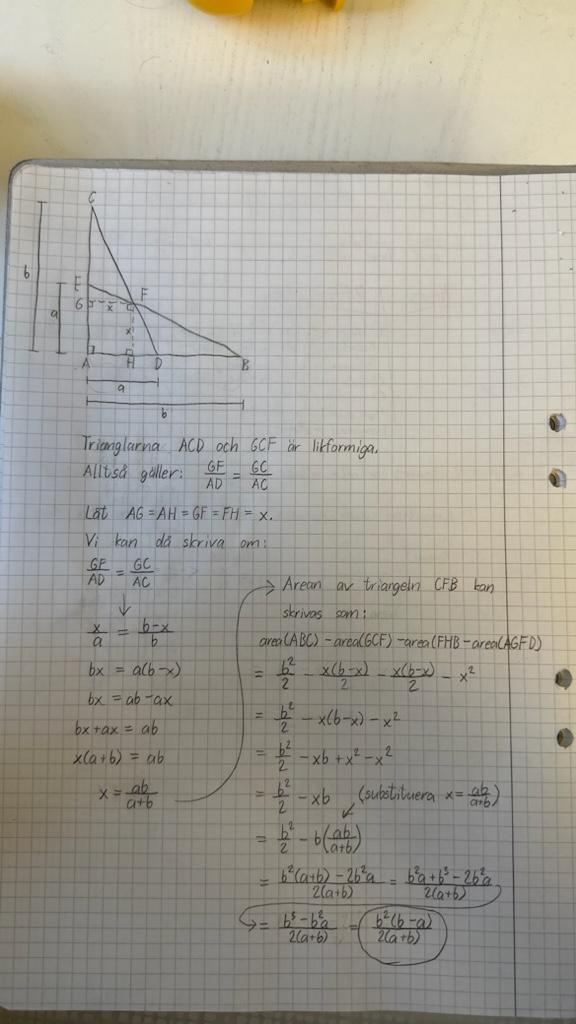
Du menar likformigheten (b-x)/b = x/a och sedan använda x för arean på den undre högra triangeln? Smart.

Jag använde likformigheten mellan den färgade triangeln och den innanför (sidförhållande b:a).
Om skärningspunkten kallas F ger det BF/FE, BF/BE och areaförhållandet mellan den sökta arean och arean av BCE. Inte mer räkningar men lite mer resonemang. Kul när det finns många olika lösningar.

skulle nån kunna skicka en fullständig lösning och posta det 

Det område som inte är färgat kan vi dela upp i två delar:

En rätvinklig triangel med arean a*b/2

En triangel med basen (b-a) och höjden x. Ser du det?

Med likformighet enligt tidigare inlägg kan vi få fram x.

Jag kommer ingen vidare. Är det här rätt tänkt eller ?

Bubo skulle du kunna posta bild. Jag förstår dig ej.

Här är ett nytt försök

Här är bokens ledtråd förresteb

tack så mycket !

Jag har en kommentar i ekv 1 skrev du :$\frac{x}{a}=\frac{b-x}{b}\leftrightarrow x=\frac{ab}{a+b}$

men borde väl inte x bli$x =\frac{ab-ax}{a+b}\leftrightarrow \frac{a(b-x)}{a+b}$?

Samla x på en sida.

$\frac{x}{a}=\frac{b-x}{b}$

$$\begin{gathered} bx=ab-ax \\ ax+bx=ab \\ x(a+b)=ab \end{gathered}$$

$x=\frac{ab}{a+b}$

Då får du samma uttryck som Trinity2.

Är det alltså korsvis multiplikation som gäller här ?

Jo, det är nog smidigast.

Det fungerar ju med att förlänga VL med b och HL med a, Ger samma resultat.

så här kan man också göra: