Arean av den ursprungliga triangeln
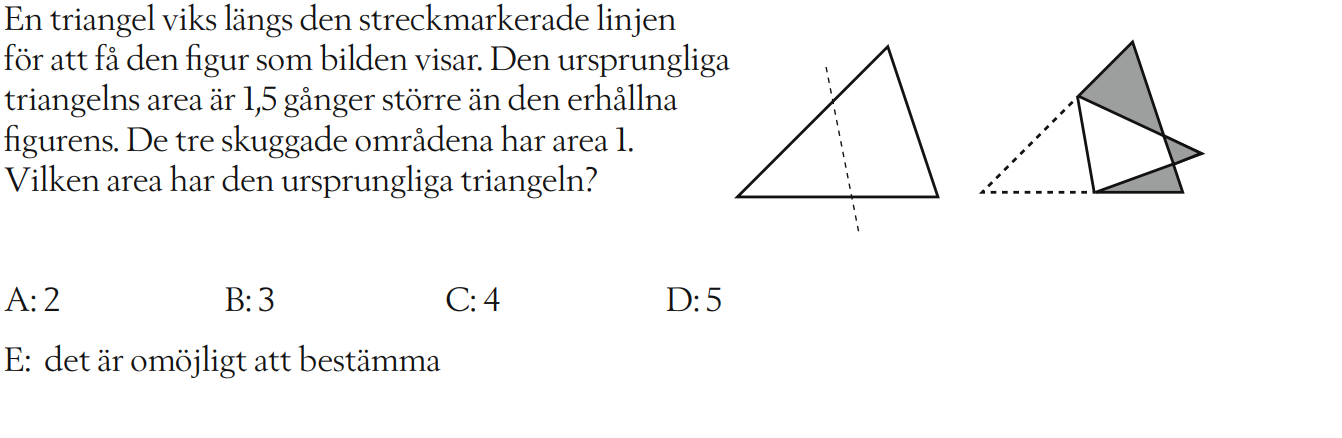
Kalla arean av det gröna området för x, och ställ upp lämpliga ekvationer.

kan jag kalla sidlämgderna för x och y så blir väl Arean
Arup skrev:kan jag kalla sidlämgderna för x och y så blir väl Arean
För att vi ska kunna svara på frågan behöver du beskriva hur du tänker.
Vilken area och vilka sidlängder?
Visa gärna.
Fortsätter på Bubos tankegång och tipsar om att vika tillbaka till en triangel, men att behålla färgmarkeringarna och samtidigt namnge respektive områdes area enligt följande. Kan det hjälpa dig vidare?

Bubo skrev:Kalla arean av det gröna området för x, och ställ upp lämpliga ekvationer.
Vad innebär "lämliga" ekvationer ?
Arup skrev:Vad innebär "lämliga" ekvationer ?
Pröva med något som har med arean att göra.
Du vet att den ena figurens area är 1,5*den andra figuren area.
Yngve kan vi ta det på räknestugan nästa vecka
Enl. figur i #5: D=E
Enl. uppg: A+B+C+D+E = 1.5(A+B+C+E) och A+B+C=1
Alltså 1+2E=1.5(1+E) vilket ger E=1 vilket ger D=1 vilket ger sökt area = A+B+C+D+E=1+1+1=3.
@Trinity 2 har du en bild du kan visa för att demonstrera hur du har löst uppgiften. Jag tycker det blir enklare att följa med på så vis
Bra lösning. Så här lyder lösningförslagen :
"Låt den oskuggade ytan i den erhållna figuren ha arean a. Då vet vi att triangelns areaär 1,5 (a+1). Viker vi tillbaka, så består triangeln av de två oskuggade delarna, varderamed area a och de tre skuggade delarna med sammanlagda arean 1. Det ger följandeekvation: 1,5 (a+1)=2a+1 med lösning a=1. Triangelns area är 3 "



