Area/funktion/def.mängd och maxarea av rektangel (Matematik/Matte 3)

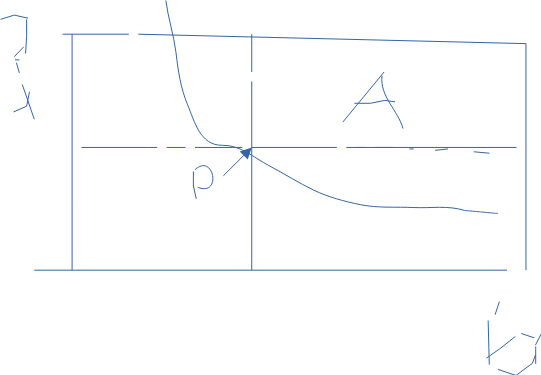
Henrik, detta ger ett helt förvirrat intryck...
Jag förstår inte vad du menar.

"Hörnpunkten P på kurvan y=4/x²med linjen y=3 och linjen x=6.
Det finns inga hörn på den kurvan. Med linjer?

När punkten P förflyttas förändras rektangelns area.
Det finns ingen hörnpunkt P . Vilken rektangel är det fråga om?

Bestäm funktion för A uttryckt i en variabel och bestäm definitionsmängd.
Vad menas med A? Vilken variabel avses? Den okända funktionens definitionsmängd?

Lägg in originaltexten så vi kan se vad som menas.

Hej Henrik. Tidigare idag skrev jag i detta svar att jag ville att du skulle spara länkar till och/eller bilder på de uppgifter du vill ha hjälp med och sedan lägga upp länkarna/bilderna tillsammans med dina frågor.

Allt för att spara tid både för dig och för oss samt att minska förvirringen som ofta uppstår kring dina trådar.

Du skrev då i detta svar att du skulle försöka göra det.

Men nu gör du samma sak igen, dvs lägger ut en otydlig fråga utan vare sig länkar eller bilder.

Min fråga till dig är: Varför gör du så?

För att detta e vad jag har o som jag sagt x antal gånger,har jag inte tillgång till bilder eller länkar, jag kan inte länka til något som jag inte har. Länkar o bilder om jag har tillgång till det, när jag kan o har tillgång till det, men till dessa har jag dessvärre det inte.

Det är kråkfötter på bild/graf, men uppgiften löd/lyder på detta sätt.

Sorry det var linjen y=3 (dvs höjden) o linjen x=6 är (basen) som kurvan (4/x²) då går genom även fast jag inte ritat kurvan fullt ut genom x=6. Det e nog också det/den som förvirrar tror jag lite också här,. Det skulle inte läggas i den meningen men bara påpekade att y=3 o x=6 som jag skrivit ut med kråkfötter.

Hörnpunkten P (pilen) finns på kurvan y=4/x²och den finns i ena hörnet av rektangeln A, ops nu blev det svart text.

A är rektangeln.

Variabel och def.mängd e det som frågas om o som jag inte vet något om.

Mvh/H

Beklagar, Henrik, men detta är inte till någon hjälp.
Dina minnesbilder av uppgiften är alltför vaga.

Lägg in originaltexten så vi kan se vad saken gäller.
Kan du inte det, bör du avsluta tråden,

Henrik 2 skrev:
För att detta e vad jag har o som jag sagt x antal gånger,har jag inte tillgång till bilder eller länkar, jag kan inte länka til något som jag inte har. Länkar o bilder om jag har tillgång till det, när jag kan o har tillgång till det, men till dessa har jag dessvärre det inte.

Jag tror att du hittade denna uppgift efter min uppmaning till dig att spara länkar och bilder.

@Henrik:

Här är en figur med kurvan y=4/x²(röd)
och linjerna y=3 (blå)
och x=6 (grön)

Punkten P ska ligga på kurvan och möjligen vara hörnpunkt i en rektangel,
men mer får vi inte veta om denna rektangel

Det är så långt jag kommer med dina uppgifter.

Nu blev denna ännu mer kråkfötter för programmet lät mig inte skapa siffror o göra linjer, så denna får duga.

Vd är det för program du använder? Det verkar som om du skulle behöva ett annat program. Har du prövat Geogebra och/eller Desmos, som vi har tipsat dig om flera gånger?

Jag förmodar att du vänder dig tll Henrik.
Själv använde jag här Desmos :-)

Ja, det var Henrik jag citerade.

Hej alla,

Tack för input för denna behöbver jag faktiskt hjälp med, kan ingenting om den o den e viktig för min förståelse av lite svårare uppgifter.

Ok, tack fär att du ritade kurvan o linjen y o x. Men jag har ju satt ut rektangeln A i nordöst ser ni inte det o hela den är rektangeln A med hörnpukten P i hörnet som e nere till vänster, som ligger på kurvan, framgår inte det?

Mvh/H

P.s jag har inte använt mig ,som ni märker, av Desmos eller GG men för att det ska bli klarare får jag försöka att lära mig det.

Vilken av dina vågräta linjer är. y= 3 ?
Vilken av dina lodräta linjer är x= 6 ?
Vilka är de övriga två linjerna?

Det måste du också berätta för att vi ska kunna se vilken rektangel det är fråga om.

Jag tolkar bilden så här. Är det rätt Henrik?

Får du använda digitala hjälpmedel för att hitta maximum?

Hej,

Nej, inga digitala hjälpmedel alls får användas, så handlar om det plus att jag väl e lite lat o lära mig Desmos och GG. Ja,Y, det stämmer förutom att x=6 e ju basen på x-axeln e du/ni med?

Jag har gett den info som jag har, o som faktiskt det var kanske glömt något, så borde gå o lösa o spekulera i tycker jag. Behöver kunna lösa denna.

Mvh/H

Henrik 2 skrev:
[...] plus att jag väl e lite lat o lära mig Desmos och GG.

Har du prövat Desmos? Det är väldigt enkelt och inte alls svårt att lära. Jag tror att både du och vi sparar mycket tid och förvirring om du tar dig den tiden.

Rita i Desmos, ta en screenshot, lägg upp bilden här. Mycket snabbare och bättre än att du ritar för hand i något ritprogram på datorn.

Ja,Y, det stämmer förutom att x=6 e ju basen på x-axeln e du/ni med?

Nej, vad menar du med det, kan du visa med bild?

Jag har gett den info som jag har, o som faktiskt det var kanske glömt något, så borde gå o lösa o spekulera i tycker jag. Behöver kunna lösa denna

Börja med att ange koordinaterna för punkten P.

Säg att x-koordinaten ör x. Kan du då komma på vad y-koordinaten är, uttryckt i x?

Ok, kikar in på Desmos då, vad e länken till den, kan ni skicka.

Ja, men e det lite svårt att lära sig det,eller inte alls för någo som inte e så kunnig..:)

Jag får nämligen en tredjegradsekvation, men jag kan ha gjort fel.

Angående x så är det väl den du pekar på, men för mig känns det som en höjd. x utgår från x-axeln men man kan peka på det sättet också,men jag hade pekat på att x=6 ligger på x-axeln.

Har inga koordinater för punkten P, fanns inte ,om jag kommer ihåg, i frågan.

Henrik 2 skrev:
Ok, kikar in på Desmos då, vad e länken till den, kan ni skicka.

Ja, men e det lite svårt att lära sig det,eller inte alls för någo som inte e så kunnig..:)

Desmos.com

Mycket enklare än din grafräknare. Pröva!

Henrik 2 skrev:
Angående x så är det väl den du pekar på, men för mig känns det som en höjd. x utgår från x-axeln men man kan peka på det sättet också,men jag hade pekat på att x=6 ligger på x-axeln.

x = 6 är en vertikal linje.

y = 3 är en horisontell linje.

Har inga koordinater för punkten P, fanns inte ,om jag kommer ihåg, i frågan.

Nej, det är inte några fasta koordinater.

Du vet att sambandet mellan x och y är y = 4/x²

Ok, så kanske det är då x=6 vertikal ,vet o förstår att y=3 är horisontell.

Samband,ja för kurvan går genom dem båda.

Alla punkter (x, y) som ligger på kurvan uppfyller sambandet y = 4/x²

Punkten P har koordinaterna (x, y).

Eftersom punkten P ligger på kurvan så har P koordinaterna (x, 4/x²).

Är du med då?

Ok, så den/P har samma koordinat som kurvan.

Så hur tacklar man denna fråga,två olika saker som efterfrågas här?

Du har en rektangel vars area A du ska maximera.

Tre av rektangelns hörnpunkter har välkända koordinater. Det nedre vänstra hörnet (vid punkten P) har koordinaterna (x, 4/x²).

Första steget är att uttrycka rektangelns area med hjälp av x.

Hm, tre, inklusive eller exlusive punkten ps hörn?

Den nedersta vid punkten P o kurvan 4/x² ,den översta på x=6 linjen koordinat, 6,3, och viken är den tredje o fjärde?

Arean med hjälp av x,ok......kan inte..

Mvh/H

Henrik 2 skrev:
Hm, tre, inklusive eller exlusive punkten ps hörn?

Den nedersta vid punkten P o kurvan 4/x² ,den översta på x=6 linjen koordinat, 6,3, och viken är den tredje o fjärde?

Nej, fel av mig.

Det är endast ett av hörnen som har kända koordinater, nämligen det övre högra, med koordinaterna (6, 3).

Det nedre vänstra hörnet har koordinaterna (x, 4/x²).

Arean med hjälp av x,ok......kan inte..

Det är en rektangel.

Dess area är längd gånger bredd.

Uttryck längden, dvs avståndet mellan vänstra och högra sidan, med hjälp av x.

Uttryck bredden, dvs avståndet mellan övre och undre sidan, med hjälp av x.

Multiplicera dessa uttryck med varandra.

Då får du, med hjälp av x, ett uttryck för rektangelns area.

Vet inte vilka mått det är vare sig basen eller höjden. Har punkten Pmed koordinater x,4/x² som då är x o y koordinat i vänstra hörnet o sedan är det x=6 till höger hur får man ut något av detta för bredd/bas?

Höjden har vi y=3 o sedan y-koordinaten på P var 4/x²sade du?

Hur får man ut en funktion för arean i rektangen av A av det?

Mvh/H

Se figuren i #13.
Rita rektangeln på nytt (på papper)

Nedre vänstra hörnet är P som har koordinaterna (x, 4/x²)
Övre högra hörnet har koordinaterna (6, 3).
Se figuren i #13

Rektangels bas är då avståndet mellan P och (6, 4/x²).
Rektangels höjd är då avståndet mellan P och (x, 3)
Se figuren i #13

Ställ upp uttryck för basen och höjden (båda innehåller x).
Du får ett uttryck för rektangelns area genom att multiplicera ihop dessa uttryck.
(Även detta uttryck innehåller x .)

Ok, lyssnar o läser men vet inte hur man beräknar detta avstånd mellan dessa punkter o vad funktionen o sedan maxareqn blir.

Mvh /H

OK vi kallar det för bas och höjd istället för längd och bredd.

=== Tolkning av uppgiften ===

Det finns flera möjliga rektanglar, beroende på var på grafen y = 4/x² som punkten P ligger.

Vi tolkar uppgiften som att punkten P ligger i första kvadranten, tll vänster om linjen x = 6 och under linjen y = 3.

Alltså som bilden nedan visar.

==================

I så fall får vi att:

Basen är avståndet mellan den vänstra vertikala sidan (med x-koordinat x) och den högra vertikala sidan (med x-koordinat 6). Detta avstånd är 6-x.

Höjden är avståndet mellan den undre horisontella sidan (med y-koordinat 4/x²) och den övre horisontella sidan (med y-koordinat 3). Detta avstånd är 3-4/x².

Basen är alltså 6-x och höjden är 3-4/x².

Rektangelns area A är basen gånger höjden, dvs A = (6-x)(3-4/x²).

Hängde du med på detta?

Yes, perfekt, har sett hur man tar minus på detta sätt för att få reda på avståndet mellan dessa punkter, så e med på detta.

Frågorna löd:

Bestäm funktion för A uttryckt i en variabel och bestäm definitionsmängd.

Bestäm rektangelns maxarea med hjälp av funktionen för arean.

Är detta funktionen för A eller beräknar man denna för att få fram arean och funktionen?

Och om så hur bestämms maxarean om o när punkten på förflyttas som också stod i uppgiften?

Mvh/H

Henrik 2 skrev:
Yes, perfekt, har sett hur man tar minus på detta sätt för att få reda på avståndet mellan dessa punkter, så e med på detta.

Vad bra!

Frågorna löd:

Bestäm funktion för A uttryckt i en variabel och bestäm definitionsmängd.

Bestäm rektangelns maxarea med hjälp av funktionen för arean.

Är detta funktionen för A eller beräknar man denna för att få fram arean och funktionen?

Vad menar du med "detta"?

Skriv ut det du menar så slipper vi gissa.

Och om så hur bestämms maxarean om o när punkten på förflyttas som också stod i uppgiften?

Det beror på hur uttrycket för arean ser ut.

Jag vet inte vad du menar nu, har bara den infon som finns i inlägg 1. Du har ju tolkat hur det ser ut precis som det ska vara, tror jag, men uppgiften löd på detta sätt, mer eller mindre. Där a o b-frågorna löd

Bestäm funktion (arean) för rektangeln A uttryckt i en variabel och bestäm definitionsmängd.

Bestäm rektangelns maxarea med hjälp av funktionen för arean.

Du skrev

Rektangelns area A är basen gånger höjden, dvs A = (6-x)(3-4/x²).

Är detta funktionen (arean) för A eller ska man beräkna denna i en variabel? Def.mängd?

Hur får man ut maxarean med hjälp av funktionen?

Henrik 2 skrev:
Jag vet inte vad du menar nu, har bara den infon som finns i inlägg 1. Du har ju tolkat hur det ser ut precis som det ska vara, tror jag, men uppgiften löd på detta sätt, mer eller mindre. Där a o b-frågorna löd

Bestäm funktion (arean) för rektangeln A uttryckt i en variabel och bestäm definitionsmängd.

Bestäm rektangelns maxarea med hjälp av funktionen för arean.

Du skrev

Rektangelns area A är basen gånger höjden, dvs A = (6-x)(3-4/x²).

Är detta funktionen (arean) för A eller ska man beräkna denna i en variabel? Def.mängd?

Ja, A(x) = (6-x)(3-4/x²) är areafunktionen, uttryckt i en variabel, nämligen variabeln x.

Hur får man ut maxarean med hjälp av funktionen?

Multiplicera ihop parenteserna och försök att använda någon standardmetod för att hitta största värdet.

Ok, så det är areafunktionen med en variabel, dvs x. Vad är def.mängden då som också efterfrågades. def.mäng det var x-värden?

Ok, testar att muitplicera ihop dem. Hm, derivering o sätt till 0 var det så för att kika max,minpunkt?

Mvh/H

Henrik 2 skrev:
Ok, så det är areafunktionen med en variabel, dvs x. Vad är def.mängden då som också efterfrågades. def.mäng det var x-värden?

Ja, definitionsmängden består av alla tillåtna x-värden.

Ok, testar att muitplicera ihop dem. Hm, derivering o sätt till 0 var det så för att kika max,minpunkt?

Det är en bra standardmetod. Pröva och visa dina uträkningar

multiplicera

Så hur blir det med def.mängd i denna fråga/svar?

Så jag multiplicerar ihop parenteser. Sedan deriverar o sätter jag till 0?

Mvh/H

Hm, när man multiplicerar 6an med -4/x²e det bara täljaren som mulpliceras med 6an o samma sak -x multiplicerat med -4/x²är det bara i täljaren som det sker en multiplikation?

Mvh/H

Hej Henrik,

Om du ska utföra denna multiplikation kan du tänka så här:

$\frac{6}{1} \cdot \frac{- 4}{x^{2}} = \frac{6 \cdot - 4}{1 \cdot x^{2}} = \frac{- 24}{x^{2}}$

Regeln för multiplikation med bråk är att täljarna multipliceras var för sig och nämnarna var för sig.

Dessa regler måste sitta som rinnande vatten för högre betyg i Ma3. Om du känner dig osäker, först och främst, tveka inte att fråga. Sedan kan det vara en idé att repetera formelbladet på nytt.

Lycka till.

Henrik 2 skrev:
multiplicera

Så hur blir det med def.mängd i denna fråga/svar?

Fundera själv.

Finns det någon undre gräns för vilket värde x kan ha?
Finns det någon övre gräns för vilket värde x kan ha?

Så jag multiplicerar ihop parenteser. Sedan deriverar o sätter jag till 0?

Ja, pröva det.

Henrik 2 skrev:
Hm, när man multiplicerar 6an med -4/x²e det bara täljaren som mulpliceras med 6an o samma sak -x multiplicerat med -4/x²är det bara i täljaren som det sker en multiplikation?

Ja.

Tack alla, hej Mesopotamia, hur har det gått med allt,var det i 2an du går o som du nu precis gått ut, så 3an nu sista året?

Då tänker jag som 6/1 o således så var det som jag sade korrekt denna gång med 6an som enbart multipliceras med täljaren 1 med nämnaren.

Hm, så gränsvärde i denna fråga/svar. Kikar man på 4/x²som går mot oändligheten o ingen övre gräns?

Undre gräns,nej vet inte riktigt just nu,kommer inte ihåg. Kommer kanske på det om du säger det då jag kikat video på detta.

Testar nu att mulplicera ihop parenteser o därefter derivererar o sätter till 0 o se vad som jag får.

Jag får 6x-(24/x²)-(x²)+(4x/x²) e detta korrekt o om så ska jag förenkla o flytta upp x²till täljaren innan jag deriverar o sätter till 0?

Mvh/H

Få se... $(6 - x) (3 - \frac{4}{x^{2}}) = 18 - \frac{24}{x^{2}} - 3 x + \frac{4 x}{x^{2}} = 18 - \frac{24}{x^{2}} - 3 x + \frac{4}{x}$ så ditt uttryck stämmer inte.

Vad menar du med "förenkla o flytta upp x² till täljaren"? Om du menar att du kan förkorta termen 4x/x² med x så att det blir 4/x så stämer det, men jag har svårt att få till den tolkningen av det du har skrivit.

När du skall derivera uttryckete så underlättar det om du skriver 24/x² som 24x^-2 och 4/x som 4x^-1 så kan du använda den vanliga regeln för att derivera åotenser.

Nej, nu tog jag fel skrev ett x istället för 3 så gör om det,o /eller kikar på din beräkning.

Mvh/H

Det var så jag menade att jag flyttar upp dessa till täljaren, man kanske inte kallar det förenkla, men precis så behöver man göra innan man deriverar som underlättar.

Det här med def.mängd med övre o undre gräns hur tolkar man det i frågan, förstår att det e något med 4/x²?

Mvh/H

Henrik 2 skrev:
Det här med def.mängd med övre o undre gräns hur tolkar man det i frågan, förstår att det e något med 4/x²?

Titta på bilden.

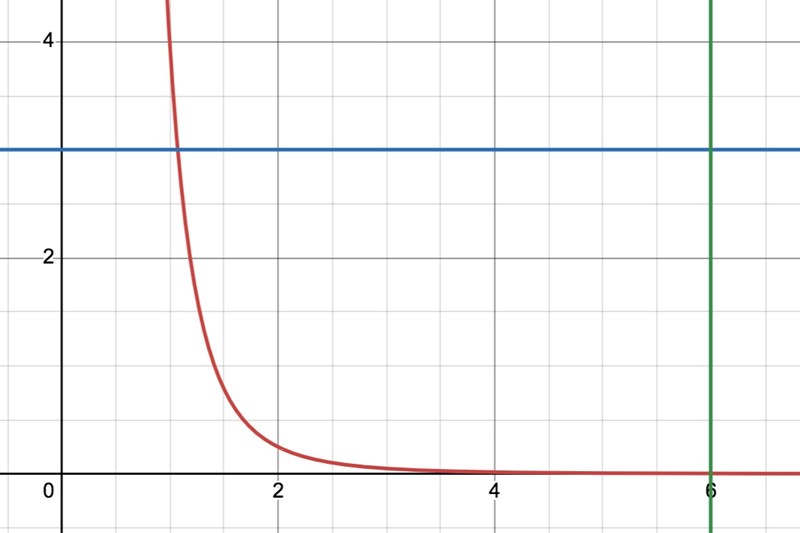
Här ser du att x inte kan vara större än 6, och att det minsta x-värdet är lite större än 1 (för att få reda på det exakta värdet behöver vi lösa ekvationen 4/x² = 3). Där har du definitionsmängden.

Du kan också se att y-värdena ligger mellan 0 och 3. Där har du värdemängden.

Att försöka lösa den här uppgiften utan att börja med att rita är som att ta på sig ett par slalompjäxor innan man skall simma över Engelska kanalen.

Vet dock inte om jag förståt tolkning. Ser att kurvan plattar ut o ligger på linjen y=0 men hur menar man att x inte kan vara större än 6?

Ska man beräkna 4/x²=3 för exakta def.mängden, o. Men hur tolkar man detta, kurvan =linjen 3 eller vad e 3?

Ligger y-värdena mellan 0-3 för att linjen 3 e den blå linjen?

Som ni hör e jag lite lost nu angående hur man tolkar denna graf.

Mvh/H

Har beräknat det o fick 1,15. Så tolkar man,jag det som att enligt grafen/kurvan så är det minsta x-värdet ca 1, hur man nu ser det, o det största e 6 som e utsatt. 1 kommer man fram till genom höjden, men man sätter 3-4x²till 3=4x²men varför vet jag inte.

Mvh/H

Är defmängden ett intervall kan man säga där man titar på det största respektive det minsta x-värdet som kan antas?

Ok, fick det till 18-24x²-3x+4x^-1

A prim (x)= 48x³ -3-4x^-2

Korrekt?

Om så sätter man det till = 0 men det går ju inte?

Mvh/H

Jag får nästan samma, men 24/x², inte 24x².

Men du kanske gör rätt, men bara glömde skriva minustecknet i x^-2?

Ja, jag har t o m skrivit det här, menar 24X^-2 som när man deriverar blir 48x^-3

Men hur gör man detta om man ska sätta det till 0 o derivera?

Mvh/H

Henrik 2 skrev:
Ja, jag har t o m skrivit det här, menar 24X^-2 som när man deriverar blir 48x^-3

Men hur gör man detta om man ska sätta det till 0 o derivera?

Mvh/H

Din derivata är inte korrekt (du har tappat bort ett minustecken). Och i matematik är X och x två olika variabler (men det är ganska korkat att använda båda i samma sammanhang).

det skulle inte vara stor o litet x,felskrivet av mig. Vilket minustecken har jag tappat ?

Det e redan redigerat i inlägg 53 väl?

Mvh/H

Derivatan av f(x) = xⁿ är f'(x) = nx^n-1, inte -nx^n-1.

Henrik 2 skrev:
Vet dock inte om jag förståt tolkning. Ser att kurvan plattar ut o ligger på linjen y=0 men hur menar man att x inte kan vara större än 6?

Om x > 6 så kommer punkten P att ligga på fel ställe enligt tolknigen i svar #31

Ska man beräkna 4/x²=3 för exakta def.mängden, o. Men hur tolkar man detta, kurvan =linjen 3 eller vad e 3?

P måste ligga på den del av grafen till y = 4/x² som ligger i första kvadranten, under linjen y = 3 och till vänster om x = 6.

Det gör att x-koordinaten för P måste vara större än det x-värde som löser ekvationen 3 = 4/x² och mindre än 6.

Annars hamnar P på fel ställe.

Ligger y-värdena mellan 0-3 för att linjen 3 e den blå linjen?

Nej, y-värdena är inte intressanta här.

Som ni hör e jag lite lost nu angående hur man tolkar denna graf.

Det ska bli en rektangel enligt tolkningen i svar #31.

Därför måste de tillåtna x-värdena begränsas. Denna begränsning blir till definitionsmängden.

Henrik 2 skrev:
Ok, fick det till 18-24x²-3x+4x^-1

A prim (x)= 48x³ -3-4x^-2

Korrekt?

Om så sätter man det till = 0 men det går ju inte?

Mvh/H

Jag tror inte detta är rätt väg att gå i denna uppgift. Ekvationen har ingen exakt lösning. Därmed är nog uppgiften ämnad för grafisk lösning av det lokala extremat.

Ja, ok, x-värden måste begränas iom att det ska bli en rektangel.

Förstod inte formeln som Smaragdalena skrev i inlägg 56. Vad o vart e felet i denna derivata A(x)?

- *-=+ och -*+=+ som då e gjort med x^-2och x^-1e det fel?

A(x)= 18-24x^-²-3x+4x^-1och

A prim (x)= 48x^-³ -3-4x^-2

Laguna fick samma derivata som jag så vad e felet,ge mig det konkret så jag ser o förstår,tack.

Nej om denna derivata e korrekt så går den väl inte att lösa algebraiskt, ska man ta grafräknaren för att lösa den?

Mvh/H

Henrik 2 skrev:
Ja, ok, x-värden måste begränas iom att det ska bli en rektangel.

Förstod inte formeln som Smaragdalena skrev i inlägg 56. Vad o vart e felet i denna derivata A(x)?

- *-=+ och -*+=+ som då e gjort med x^-2och x^-1e det fel?

A(X)= 18-24x^-²-3x+4x^-1och

A prim (x)= 48x^-³ -3-4x^-2

Den derivatan stämmer - två minus blir till plus. Det du påstod innan var något annat.

Laguna fick samma derivata som jag så vad e felet,ge mig det konkret så jag ser o förstår,tack.

Nej om denna derivata e korrekt så går den väl inte att lösa algebraiskt, ska man ta grafräknaren för att lösa den?

Bra idé.

Ok, så denna går ej att lösa algebraiskt, nej förstår inte hur man skulle göra det.

Så hur gör man den på grafräknaren, plottar man? O sedan vad, den ska ju sättas till 0 också för att se min/maxpunkt?

Mvh/H

Desmos: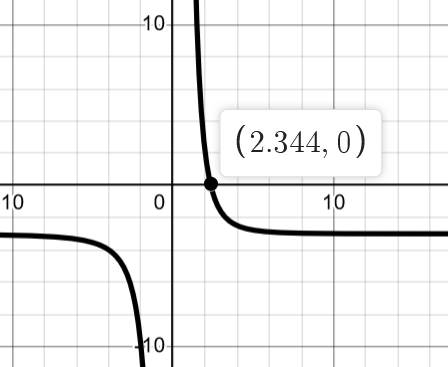

Smaragdalena har matat in funktionen och fört sitt finger över funktionen där den y=0, eller använt knappen där man får fram nollstället.

Vet du hur man gör?

Jag föreslår att du slår in funktionen g(x)=3x³+43 och ser om du kan hitta nollstället med hjälp av antingen Desmos eller Geogebra.

Själv föredrar jag Geogebra, men det är en smaksak.

Vi får inte ha dessa hjälpmedel på provet ,kan kika i Desmos men behöver lösa denna på grafräknare, har en T-82-STATS. Kan ni hjälpa mig hur man gör det o slår in kommandon?

fört finger över y=0,vad menas? Vart finns nollstället i Desmos?

Jag skriver in funktionen i rutan och sedan vart hittar jag nollstället?

Har skrivit in den men vet inte hur jag navigerar mig till knappen för nollstället.

Är detta en maxpunkt på 2.344?

Mvh/H

Om du skriver in funktionen i Desmos kan du klicka på punkten där kurvan skär x-axeln (d v s där y = 0) så får du fram koordinaterna.

Just det, testa o funkade,fint. Men får inte ha digitala hjälpmedel på provet, så hur gör man detta på grafräknaren?

Och är det en maxpunkt eller minpunkt?

Vad är maxarean som efterfrågas?

Mvh/H

Skriv in derivatan i räknaren. Leta upp skärningen med x-axeln.

Skriv in själva funktionen i räknaren och titta på grafen, så ser du om det är ett max eller min.

Ok, men behöver navigering. ska man skriva in derivatan o plotta det o sedan kika grafen.?

Glömde e det på MATH eller Calc som man kikar min/maxpunkt o vilket alternativ?

Mvh/H

Ps. så om det e en maxpunkt e det maxarean då som vi har i derivatan/funktionen?

Vet inte om jag fick rätt x-värde o fick olika o vet inte heller riktigt kommandon på grafräknaren.

Så denna kan inte lösas algebraiskt med att räkna ut maxarean?

Ser inte om det e max,min då det e två olika linjer/ekvationer man får, som ni ser i inlägg 62?

Mvh/H

Det är faktiskt $2(\sqrt[3]{1+\frac{\sqrt{730}}{27}}+\sqrt[3]{1-\frac{\sqrt{730}}{27}})$ .

Hej Henrik,

Jättebra att du provade på Desmos.

Jag förstår dock inte när du skriver "vi får inte ha digitala hjälpmedel på provet". Det är väl NP du syftar på? Där är det sjävklart att man får använda digitala hjälpmedel.

Har din skola förbjudit sådana och endast tillåter grafritande miniräknare? Det låter väldigt märkligt, eftersom Skolverket har många exempel på Geogebra och liknande i sina lösningsförslag till proven, dvs. verktygen är inte något som endast få skolor använder.

Hej

Det stämmer vi har o kommer inte ha tillgång till det om jag gör prövning igen hos den aktör jag gör det hos . Så med det hur beräknar man denna med grafräknare vet ni?

Mvg/H

Jag kan tyvärr inte hjälpa dig med räknaren, men har en fundering:

Har du frågat skolan om du får ta med dig en egen dator där du kan använda det digitala hjälpmedlet?

Henrik 2 skrev:
Hej

Det stämmer vi har o kommer inte ha tillgång till det om jag gör prövning igen hos den aktör jag gör det hos . Så med det hur beräknar man denna med grafräknare vet ni?

Mvg/H

Vad är det för en aktör du studerar hos? Har du frågat dem varför de inte följer Skolverkets anvisningar?

Det e Jensen men även andra aktörer tror jag inte heller har. Men kan denna fråga bara lösas med GG, Desmos eller liknande digitala hjälpmedel?

Någon som vet hur man löser denna med grafräknare?

Är derivering fram till detta korrekt, e det så här man ska lösa frågan, dels funktion o dels maxarean?

Mvh/9

Du kan skriva in de aktuella funktionerna (t ex derivatan och linjen y = 0) i räknaren och undersöka var de korsar varandra, verktyget kan t ex heta intersect. När jag gick på gymnasiet löste vi sådana uppgifter med räknare som inte ens hade graffunktion - vi fick använda räknaren för att göra en värdetabell och pricka in punkterna för hand på ett rutigt papper.

Jo, försöker men får olika x värden då kurvorna e skilda från varandra. Vet inte vilken av dem man ska kika på. Dem korsar väl aldrig varandra.

Kan du ta en bild med din mobilkamera och lägga upp här? Det blir svårt att hänga med på vad du menar.

Henrik 2 skrev:
Jo, försöker men får olika x värden då kurvorna e skilda från varandra. Vet inte vilken av dem man ska kika på. Dem korsar väl aldrig varandra.

Vi har pratat om definitionsmängden tidigare, dvs vilka x-värden som är tillåtna.

Kan du säga vilka det är (helst utan att kika tillbaka i tråden)?

Hej,

Vi har ju nu fått en derivata med upphöjt till minus det måste göras algebraiskt eller digitala hjälpmedel. väl?

Är det rätt derivata...

Nu har vi kommit fram till funktion o uttryck för A o def mängd nu ska maxarean räknas ut o har kommit fram till derivatan därefter vet jag inte hur jag löser det algebraiskt eller med grafräknare.

Mvh/H

Du frågade i svar #77 vilket x-värde som ska användas eftersom kurvorna är skilda från varandra.

Då tänker jag att definitionsmängden kan vara en ledtråd till vilket x-värde som ska användas.

Vi sammanfattar det vi har kommit fram till hittills.

Enligt tolkning i svar #31 så har vi att

Punkten P har koordinaterna $(x,\frac{4}{x^2})$
Arean är $A(x)=18-\frac{24}{x^2}-3x+\frac{4}{x}$
Definitionsmängden är $\frac{2}{\sqrt{3}}<>$
Derivatafunktionen är $A'(x)=\frac{48}{x^3}-3-\frac{4}{x^2}$

Vi söker nu det maximala värdet som $A(x)$ kan anta.

För att hitta det x-värde för vilket $A(x)$ antar sitt största värde så letar vi efter stationära punkter i det tillåtna intervallet, dvs vi löser ekvationen $A'(x)=0$ och kontrollerar att lösningen/lösningarna ligger i definitionsmängden.

Med hjälp av grafräknare eller annat digitalt hjälpmedel kommer vi fram till att $A'(x)=0$ vid ungefär $x\approx2,344$ .

Detta värde ligger i definitionsmängden.

Den eftersökta maximala arean blir då ungefär $A(2,344)$

==== Kommentarer ====

Vi behöver visa att $x\approx2,344$ verkligen ger ett maxvärde.

Då kan vi resonera som så att arean går mot 0 då x går mot definitionsmängdens ändpunkter. Därför måste den stationära punkten vara en maximipunkt.

För att lösa ekvationen $A'(x)=0$ med hjälp av grafräknare så matar vi in de två funktionsuttrycken y₁ = 48/x^(-3)-3-4/x^(-2) och y₂ = 0, zoomar in så att vi ser skärningspunkten och väljer Intersect.

Min fråga till dig Henrik: Är du med på allt som står i svar #82?

Hej Y,

Perfekt med detta förtydligande, det jag behövde o som jag förstår tror att jag förstår.

Det blir väl dock inte 48/x⁽^-3) -3-4/x^(-2)=0. Det blir väl antingen 48x⁽^-3)-3-4x^(-2) =0 eller 48/x³-3-4/x²Var det ett error av dig eller av mig?

Ska plotta, zooma o sedan välja intersec o se om jag får ca 2,344.

Så om e en maxpunkt på 2,344 ska detta x sättas in då i funktionen för att få ut maxarean?

Mvh/H

P.s def.mängd så blir det minsta värdet x=1,15 o största 6 men som skrivs som du skrev det?

Henrik 2 skrev:
Hej Y,

Perfekt med detta förtydligande, det jag behövde o som jag förstår tror att jag förstår.

Det blir väl dock inte 48/x⁽^-3) -3-4/x^(-2)=0. Det blir väl antingen 48x⁽^-3)-3-4x^(-2) =0 eller 48/x³-3-4/x²Var det ett error av dig eller av mig?

Ja, jag skrev fel där. Bra fångat!

Ska plotta, zooma o sedan välja intersec o se om jag får ca 2,344.

Så om e en maxpunkt på 2,344 ska detta x sättas in då i funktionen för att få ut maxarean?

$x\approx2,344$ är ett nollställe till A'(x).

Om du sätter in det värdet i areafunktionen A(x) (dvs beräknar A(2,344)) så får du det största värdet för arean.

P.s def.mängd så blir det minsta värdet x=1,15 o största 6 men som skrivs som du skrev det?

Nej, likhetstecken duger inte. Om $x=\frac{2}{\sqrt{3}}$ så blir det ingen rektangel. Inte heller om $x=6$ .

Det måste gälla att $x>\frac{2}{\sqrt{3}}$ och att $x<6$ .

Det kan skrivas på olika sätt, varav $\frac{2}{\sqrt{3}}<>$ är ett.

Yngve skrev:

...

Det kan skrivas på olika sätt, varav $\frac{2}{\sqrt{3}}<>$ är ett.

LaTeX spökar ibland. Yngve menar att $\frac{2}{\sqrt{3}} < x < 6$ är ett sätt att skriva definitionsmängden.

Tack Smaragdalena.

LaTex gillar inte < och >.

Aha, så def.mängd ,ett intervall och då ska det skrivas på det sättet, och inte =.

Så man ska inte skriva med decimaler, som 1,15 utan då skriver man 2/roten ur 3, hur kommer man fram till det?

6 förstår jag men vad hade vi 4/x²hur blir det 2/roten ur 3, jag fick ,tror jag, roten ur 4/3=x

Precis jag sätter in detta x.värde i A(x)= A(x)=18−(24/x ²)−3x+(4/x)

Mvh/H

P.s Vad e La,Tex?

Jag tar detta på grafräknaren men då det är två lika kurvor/linjer/funktioner en över x-axeln och en under så vet jag inte hur man går med markören för att få x=2,344 när dem frågar om 1st curve, 2nd curve, o sedan guess. Vilken av dessa kurvor e första, vilken e andra?

Se inlägg 62 för graf/kruvor/linjer/funktioner

Mvh/H

Ska beräkna maxarean då jag sätter in x-värdet istället för x i A(x).

Fick arean efter jag satt det inom parentes till 43,07 dvs 43 (var det cm ,cm² ?)

Vad fick ni?

Mvh/H

Henrik 2 skrev:
Aha, så def.mängd ,ett intervall och då ska det skrivas på det sättet, och inte =.

En definitionsmängd är, som namnet antyder, en mängd. I detta fallet är det en mängd tal. Denna mängd kan beskrivas på olika sätt. Det jag skrev (eller försökte skriva) var ett sådant sätt.

Så man ska inte skriva med decimaler, som 1,15 utan då skriver man 2/roten ur 3, hur kommer man fram till det?

1,15 är ett närmevärde. $\frac{3}{\sqrt{3}}$ är ett exakt värde. Du ska i de flesta fallen försöka använda exakta värden istället för närmevärden.

6 förstår jag men vad hade vi 4/x²hur blir det 2/roten ur 3, jag fick ,tror jag, roten ur 4/3=x.

Läs svaren #47, #48 och #57 igen

P.s Vad e La,Tex?

LaTex är ett system som gör att man kan skriva uttryck som $\frac{2}{\sqrt{3}}$ direkt i texten utan att använda den formeleditor som är inbyggd i PA.

Man använder då dubbla dollartecken för att visa var ett sådant uttryck startar och slutar.

Pröva själv att t.ex. skriva x^2 omgivet av dubbla dollartecken.

Om du skriver så här:

så blir resultatet så här:

$x^2$

====

Du kan läsa mer om vad LaTex är här.

Och en utmärkt guide till LaTex på PA hör.

Ok, kikar länkar angående LaTex sedan.

Men jag förstår inte när man tar intersec vilka kurvor det är, dem sitter ju inte ihop. Den ena ligger under x-axeln och den andra ligger över så vet inte alls vilka 1a ,o 2andra kurvan e och hur man går med markören för att få det til 2,344?

Så får kika inlägg 47,48 o 57 igen för att se om jag förstår varför det blir 2/roten ur 3 som minsta värde.

Jo, jag förstår, decimaler blir närmevärde medan det som du,ni skriver e exakt

Så beräknade arean var det korrekt med 43,07?

Henrik 2 skrev:
Ok, kikar länkar angående LaTex sedan.

Men jag förstår inte när man tar intersec vilka kurvor det är, dem sitter ju inte ihop. Den ena ligger under x-axeln och den andra ligger över så vet inte alls vilka 1a ,o 2andra kurvan e och hur man går med markören för att få det til 2,344?

Den enda delen av grafen som.är intressant är den vars x-vörden ligger i definitionsmängden, dvs den del av grafen där $\frac{2}{\sqrt{3}}<>$ .

Du kan ställa window-parametrarna så att endast denna del av grafen visas

Så får kika inlägg 47,48 o 57 igen för att se om jag förstår varför det blir 2/roten ur 3 som minsta värde.

Jo, jag förstår, decimaler blir närmevärde medan det som du,ni skriver e exakt

Så beräknade arean var det korrekt med 43,07?

Jag har inte räknat ut den själv ännu.

Ok, avvaktar o se om det blev rätt angåede maxarean.

Aha, så det e såklart den som ligger ovanför x-axeln som hör till def.mängd, så den andra e inte relevant, nu förstår jag det så här i efterhand,som vanligt. Hur ställer jag in fönsterparametrarna, e det mellan xmin o xmax 1 till 10 eller vad?

Mvh/H

Jag fokuserar nu enbart på den relevanta kurvan men inget händer. Jag står på den med markören, och den frågar är det här den 1st curve,yes klickar jag, är det den 2nd curve ,ska jag stå kvar där på samma kurva eller gå ner till x-axeln eller ner till den andra kurvan?

Har ändrat fönsterinställningar så bara den relevanta fokuseras men det blir ändå error..

Mvh/H

Jag har ingen grafräknare här så jag kan inte detaljstyra dig.

Men pröva att googla "Find intersection Ti-82 <skriv in din modell på grafräknare här>"

Eller kolla här

Ok, men jag kan kika länk eller googla men förstår bara inte varför jag inte får ut det.

Så du har inte tillgång till en grafräknare?

Jag förstår inte när den frågar efter 1st o 2nd curve o sedan guess hur o var jag ska gå med markören, blir bara error när jag gör det som sagt,typiskt.

Mvh/H

Henrik 2 skrev:
Ok, men jag kan kika länk eller googla

Gör det. Säg till när du har gjort det.

men förstår bara inte varför jag inte får ut det.

Så du har inte tillgång till en grafräknare?

Inte där jag är just nu nej.

Jag förstår inte när den frågar efter 1st o 2nd curve o sedan guess hur o var jag ska gå med markören, blir bara error när jag gör det som sagt,typiskt.

Klicka på länken i svar #96 och läs det som står där. Fråga oss om allt du vill att vi förklarar närmare.

Har gjort det o kikat vad det står för TI-82-STATS o jag gör det som står, men funkar inte. Jag har fortfarande problem med om jag ska flytta markören eller inte. Så har du tillgång till en i helgen så vore det bra om du kikade o försökte hjälp mig, om så e möjigt hur man går med markörenför jag e på rätt ställe men får inte ut det o fokuserar nu bara på den relevanta kurvan som är i def.mängden.

Mvh/H

Gör du precis så här?

Och sedan så här?

I steg 5 ska du alltså använda räknarens piltangenter för att flytta markören till en punkt nära skärningspunkten.

=====

Lägg gärna upp bilder på de steg du tar och vad räknaren svarar.

Jo, precis, men då står jag bara med markören på 1st och 2nd curve utan att röra markören o sedan går jag till intersection på guess. Är den då på x-axeln och kurvan så går där dem går ihop eller vart e själva intesection, kan inte se ?

Mvh/H

Graferna är

y₁ = 48/x^(3)-3-4/x^(2)

y₂ = 0

Skärningen mellan dessa ligger på x-axeln eftersom y₂ = 0 är x-axeln.

När du kommer till "Guess?" så visas markören som en liten stjärna på en av graferna.

Du ska nu flytta markören nära skärningspn kten med hjälp av höger/vänster piltangent.

Tryck Enter så får du nörmevärden till skärningspunktens koordinater.

Gör precis som denna video visar.

Om det fortfarande inte funkar får du börja lägga upp bilder som visar hur du gör och vad som händer på räknaren.

Precis, guess o då flyttar jag den, meN vet inte vart riktigt jag ska gå med markören, från själva kurvan till intersection, ser det inte riktigt. Kikar video, tack

Jag skriver dock grafen som 48x ^(-3).........det e väl likadant bara man tar det som man flyttat upp i täljaren?

Blev arean när man satt in x=2.344 ca 43.07?

Mvh/H

Henrik 2 skrev:
Precis, guess o då flyttar jag den, meN vet inte vart riktigt jag ska gå med markören, från själva kurvan till intersection, ser det inte riktigt. Kikar video, tack

Ta en bild med telefonen och visa den här.

Jag skriver dock grafen som 48x ^(-3).........det e väl likadant bara man tar det som man flyttat upp i täljaren?

Ja, men i så fall ska du skriva 48x^(-3)

Blev arean när man satt in x=2.344 ca 43.07?

Här är det bra att fundera på om det verkar rimligt eller inte.

Titta på bilden i svar #31.

Du ser där att rektangeln måste vara mindre än 6*3 = 18 a.e.

Ser du varför?

Ett rimligt värde på arean blr då ligga mellan 0 och 18 a.e.

Ja, precis skriver in upphöjt till när jag plottar.

Jag får väl se huruvida jag kan ta en bild av grafräknaren med mobilen eller inte, har inte gjort det förut. Jag ska testa o inte göra något med markören o ebart flytta den på guess.

Hm, så vart räknade jag fel då med när jag satte in x=2,344, får kika på det då.

Jag satte in det i 18-(24/2,34)-3(2,34)+(4/2,34) men det e ju själva funktionen som det blir av

(6-x)(3-4/x²). Ska man sätta in x=2,344 i denna istället o då får under 18 a.e som e det rimliga?

Jag testar det istället.

Nu så fick jag 8,30 det e ju mer rimligt om så. Ska man sätta in det i (6-x)(3-4/x²)?

Mvh/H

Heja Henrik!

Du ska sätta in x=2,344 i A(x) = (6-x)(3-4/x²) för att få max-värdet.

Här är en bild från Desmos. Kurvan är y = A(x).
Den lodräta linjen är x = 2,3

Henrik 2 skrev:
[...]

Jag satte in det i 18-(24/2,34)-3(2,34)+(4/2,34) men det e ju själva funktionen som det blir av

Nej, då mussar du exponenterna på närmevärdet 2,344.

(6-x)(3-4/x²). Ska man sätta in x=2,344 i denna istället o då får under 18 a.e som e det rimliga?

Ja

Jag testar det istället.

Nu så fick jag 8,30 det e ju mer rimligt om så. Ska man sätta in det i (6-x)(3-4/x²)?

Mvh/H

Eftersom A(x) = (6-x)(3-4/x²) och du vill beräkna (2,344) så ska du beräkna (6-2,344)(3-4/2,344²). Det ger dig arean.

=====

Men förstår du varför arean bör vara mindre än 18 a.e?

Jag gjorde väl det o frågade om då 8,30 var svaret, tog dock 2,34 o inte 2,344?

Nja, för det e basen *höjden som e 6*3 o då ska rektangelns area vara en hel del mindre än det?

Henrik 2 skrev:

Jag gjorde väl det o frågade om då 8,30 var svaret, tog dock 2,34 o inte 2,344?

Ja, 8,3 är ett bra svar.

Nja, för det e basen *höjden som e 6*3 o då ska rektangelns area vara en hel del mindre än det?

Ja, det stämmer.

Fick du ordning på Intersect med grafräknaren?

Bra då har jag allt i denna uppgift som jag behöver veta förutom att jag inte får ordning på grafräknaren. Vet alla steg, skrivit in funktionerna y1 o y2 o står på rätt ställe.Men sedan när jag svarar yes på 1st o 2nd curve så funkar det inte när det sedan e guess. Jag går med markören till intersec, tror jag, eller så gör jag ingenting med den o svarar yes men jag får bara error oavsett vad jag gör. Så har inte fått någon ordning på det än o försökt en hel del.

Mvh/H

Blir det 2/roten ur 3 för att x= roten ur 4/3 så tar man roten ur 4 som blir två men roten ur 3 kan man inte ta o få ett exakt värde således blir det 2/roten ur 3?

Mvh/H

För att bevisa att det är en maxpunkt ska man ta A biss(x)?

Hur blir A biss här av A prim (x)= 48x^-³ -3-4x^-2?

Kunde det men nu kommer jag inte ihåg när det e upphöjt till -3 och -2 vad som det blir om man ska ta andraderivatan för att kika min/maxpunkt?

Mvh/H

Henrik 2 skrev:
Blir det 2/roten ur 3 för att x= roten ur 4/3 så tar man roten ur 4 som blir två men roten ur 3 kan man inte ta o få ett exakt värde således blir det 2/roten ur 3?

Mvh/H

Ja. Det stämmer. Då använder du denna räkneregel ur ditt formelblad:

Henrik 2 skrev:
För att bevisa att det är en maxpunkt ska man ta A biss(x)?

Nej,det är onödigt krångligt.

Det är enklare attcredonera att det endast finns en stationär punkt i definitionsmängdrn och eftersom funktionsvärdet (arean) går mot 0 när x går mot intervallets gränspunkter så måste den stationära punkten vara en maximipunkt.

Hur blir A biss här av A prim (x)= 48x^-³ -3-4x^-2?

Kunde det men nu kommer jag inte ihåg när det e upphöjt till -3 och -2 vad som det blir om man ska ta andraderviatan för att kika min/maxpunkt?

Derivatan av x^a är a*x^a-1, även om a är ett negativt tal.

Exempel:

Derivatan av x^-1 är (-1)*x^-1-1 = (-1)*x^-2
Derivatan av x^-2 är (-2)*x^-2-1 = (-2)*x^-3
Och så vidare

Henrik 2 skrev:
Bra då har jag allt i denna uppgift som jag behöver veta förutom att jag inte får ordning på grafräknaren. Vet alla steg, skrivit in funktionerna y1 o y2 o står på rätt ställe.Men sedan när jag svarar yes på 1st o 2nd curve så funkar det inte när det sedan e guess. Jag går med markören till intersec, tror jag, eller så gör jag ingenting med den o svarar yes men jag får bara error oavsett vad jag gör. Så har inte fått någon ordning på det än o försökt en hel del.

Mvh/H

Ta bilder och visa/beskriv alla steg.

Jo, så det som e upphöjt till - 3 o -2 blir det således -4 o -3 i andraderivatan men dt blir för komplext att använda sig av denna här?

Credonera innebär? Konstatera?

Hur menar du att man vet,credonerar att det bara finns en maxkpunkt i def.mängden?

Du säger:

Och eftersom funktionsvärdet (arean) går mot 0 när x går mot intervallets gränspunkter så måste den stationära punkten vara en maximipunkt.

Förstår det inte,du behöver visa.

Jag vet inte hur jag ska ta bild på en liten display på grafröknaren med mobilkameran?

Mvh/H

Henrik 2 skrev:
Jo, så det som e upphöjt till - 3 o -2 blir det således -4 o -3 i andraderivatan men dt blir för komplext att använda sig av denna här?

Jag tycker att det är onödigt, men drt är såklart helt OK att använda antingen andraderivata eller teckentabell.

Credonera innebär? Konstatera?

Det skulle stå "resonera".

Hur menar du att man vet,credonerar att det bara finns en maxkpunkt i def.mängden?

Du säger:

Och eftersom funktionsvärdet (arean) går mot 0 när x går mot intervallets gränspunkter så måste den stationära punkten vara en maximipunkt.

Förstår det inte,du behöver visa.

Eftersom derivatan endast har ett nollställe i definitionsmängden så har funktionen endast en stationär punkt I definitionsmängden.

Denna stationära punkt kan antingen vara en minimi-, en maximi- eller en terrasspunkt.

Eftersom funktionsvärdet går mot 0 vid definitionsmängdens ändpunkter och funktionsvärdet är positivt däremellan så måste den stationära punkten vara en maximipunkt.

Laborera lite själv med att rita grafen till en godtyckiig funktion

vars värde går från 0 till 0 i början o h slutet av ett intervall
där funktionsvärdet är positivt (dvs grafen ligger ovanför x-axeln) däremellan och
där funktionen endast har en stationär punkt i aktuellt intervall.

För att få till ovanstående så upptäcker du att den stationära punkten måste vara en maximipunkt.

Jag vet inte hur jag ska ta bild på en liten display på grafröknaren med mobilkameran?

Ta en bild på lite längre håll och beskär den i efterskott.

Men poäng ges också för att bevisa att det är en maxpunkt. Men vet inte hur beräkningen blir då med andraderivatan då det blir mer komplext med upphöjt till min 3 o upphöjt till minus 2 kan du visa hur man beräknar det o på detta sätt ser att det blir en maxpunkt med hjälp av andraerivatan/f biss (x)?

Eftersom funktionsvärdet går mot 0 vid definitionsmängdens ändpunkter och funktionsvärdet är positivt däremellan så måste den stationära punkten vara en maximipunkt.

vars värde går från 0 till 0 i början o h slutet av ett intervall

där funktionsvärdet är positivt (dvs grafen ligger ovanför x-axeln) däremellan och

där funktionen endast har en stationär punkt i aktuellt intervall.

Förstår inte detta , enbart att värdet är positivt, dvs över x-axeln, men det övriga kan inte jag tolka o se hur det går så du behöver rita upp så att jag kan förstå

Här får du tre kurvor som uppfyller Yngves villkor:

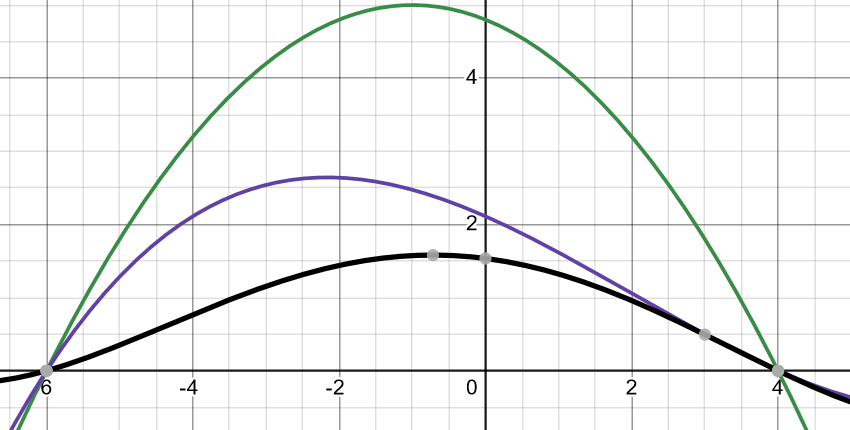
Ser du att alla har ett maximum?

Henrik 2 skrev:
Men poäng ges också för att bevisa att det är en maxpunkt. Men vet inte hur beräkningen blir då med andraderivatan då det blir mer komplext med upphöjt till min 3 o upphöjt till minus 2 kan du visa hur man beräknar det o på detta sätt ser att det blir en maxpunkt med hjälp av andraerivatan/f biss (x)?

Vi har att $A'(x)=48\cdot x^{-3}-3-4\cdot x^{-2}$

Om vi deriverar detta uttryck får vi $A''(x)=(-3)\cdot48\cdot x^{-4}-(-2)\cdot4\cdot x^{-3}=-144\cdot x^{-4}+8\cdot x^{-3}=\frac{8}{x^3}-\frac{144}{x^4}$

Andraderivatans vörde vid den stationöra punkten är då ungefär $A''(2,344)=\frac{8}{2,344^3}-\frac{144}{2,344^4}\approx0.62-4,77=-4,15$ , vilket är mindre än 0.

Alltså är den stationära punkten en maximipunkt.

Eftersom funktionsvärdet går mot 0 vid definitionsmängdens ändpunkter och funktionsvärdet är positivt däremellan så måste den stationära punkten vara en maximipunkt.

vars värde går från 0 till 0 i början o h slutet av ett intervall

där funktionsvärdet är positivt (dvs grafen ligger ovanför x-axeln) däremellan och

där funktionen endast har en stationär punkt i aktuellt intervall.

Förstår inte detta , enbart att värdet är positivt, dvs över x-axeln, men det övriga kan inte jag tolka o se hur det går så du behöver rita upp så att jag kan förstå

Jag tror att det är bättre om du ritar upp det själv.

Utgå från denna bild med helt påhittade värden, eller rita något liknande själv på ett papper.

Din utmaning:

Rita en graf från A via B till C.
Grafen ska endast ha horisontell lutning på ett enda ställe.
Du kommer då att se att det då måste vara så att grafen har en maximipunkt vid B.

Säg till när du har gjort den övningen och berätta gärna vad du kom fram till.

Andraderivatan

Tackar för kurvor mm. När du deriverar till A biss (x) så e jag med o man tar således bort 3an o så blir minus*minus +. Du sätter 8/x³före när du fortsätter, spelar det någon roll vad som sätts först,svaret blir detsamma nej det blir det väl inte?

Är det bara för att det är -144 o då väljer man att sätta den efter?

Man flyttar ner x till nämnaren igen för att kunna lösa det när 2,344 beräknas,ok.

Beräknar o ser om jag får samma svar, det fick jag.

Vad menas med detta nedan som du skrev:

vars värde går från 0 till 0 i början o h slutet av ett intervall?

Mvh/H

Henrik 2 skrev:
Andraderivatan

Tackar för kurvor mm. När du deriverar till A biss (x) så e jag med o man tar således bort 3an o så blir minus*minus +. Du sätter 8/x³före när du fortsätter, spelar det någon roll vad som sätts först,svaret blir detsamma nej det blir det väl inte?

Är det bara för att det är -144 o då väljer man att sätta den efter?

Ja, det är "snyggare" att skriva b-a istället för -b+a.

Man flyttar ner x till nämnaren igen för att kunna lösa det när 2,344 beräknas,ok.

Det behövs egentligen inte, jag gjorde det bara för tydlighets skull

Beräknar o ser om jag får samma svar, det fick jag.

Bra.

Vad menas med detta nedan som du skrev:

vars värde går från 0 till 0 i början o h slutet av ett intervall?

Se bild i svar #121. Grafen ska gå från y-värdet 0 vid punkten A till y-värdet 0 vid punkten C.

Kikar bild i 121.

Aha, 0 på y-värdet,e med på det.

Mvh/H

Bra. Har du genomfört utmaningen från slutet av svar #121?

Vad kom du i så fall fram till?

Hej,

Den e väl bara att rita en funktion, linje så ser Ms. att det blir en maxpunkt.

Mvh/Henning

Denna uppgift e löst nu men behöver bara lösa att få ut intersec 2,344 på grafräknaren.

Mvh/H

Yngve skrev:

Ta bilder och visa/beskriv alla steg.

Henrik 2 skrev:
Den e väl bara att rita en funktion, linje så ser Ms. att det blir en maxpunkt.

Ja, det var just det jag ville att du skulle upptäcka själv, med hjälp av ett grafiskt resonemang.

Om du kan beskriva detta med ord och en principiell skiss som illustration så behöver du inte använda vare sig andraderivata eller teckentabell för att påvisa att den stationära punkten måste vara en maximipunkt.

Jo, men ibland förstår jag inte vad du skriver o kan inte tolka det, så svårare i ord ibland än att se det, som ni försöker påpeka för mig då jag ska rita upp för förståelse

Nu ska jag, om linjär optimering med syltburkar o saftflaskor, försöka lösa punkt 4 med additions eler substitutionsmetoden o även hitta p5 o p6 sedan har vi nog löst för denna gång mina uppgifter såväl grafiskt,med grafräknare o algebraiskt.

Mvh/H