Area för cirkelskiva
Någon som har tips på att resonera fram radien (och sin tur arean) här? Känns som jag glömt något extremt självklart. Letar runt på “omskrivna cirklar” men hittar inget. Här är min skalenliga bild som jag ej hade kunnat göra på tenta:
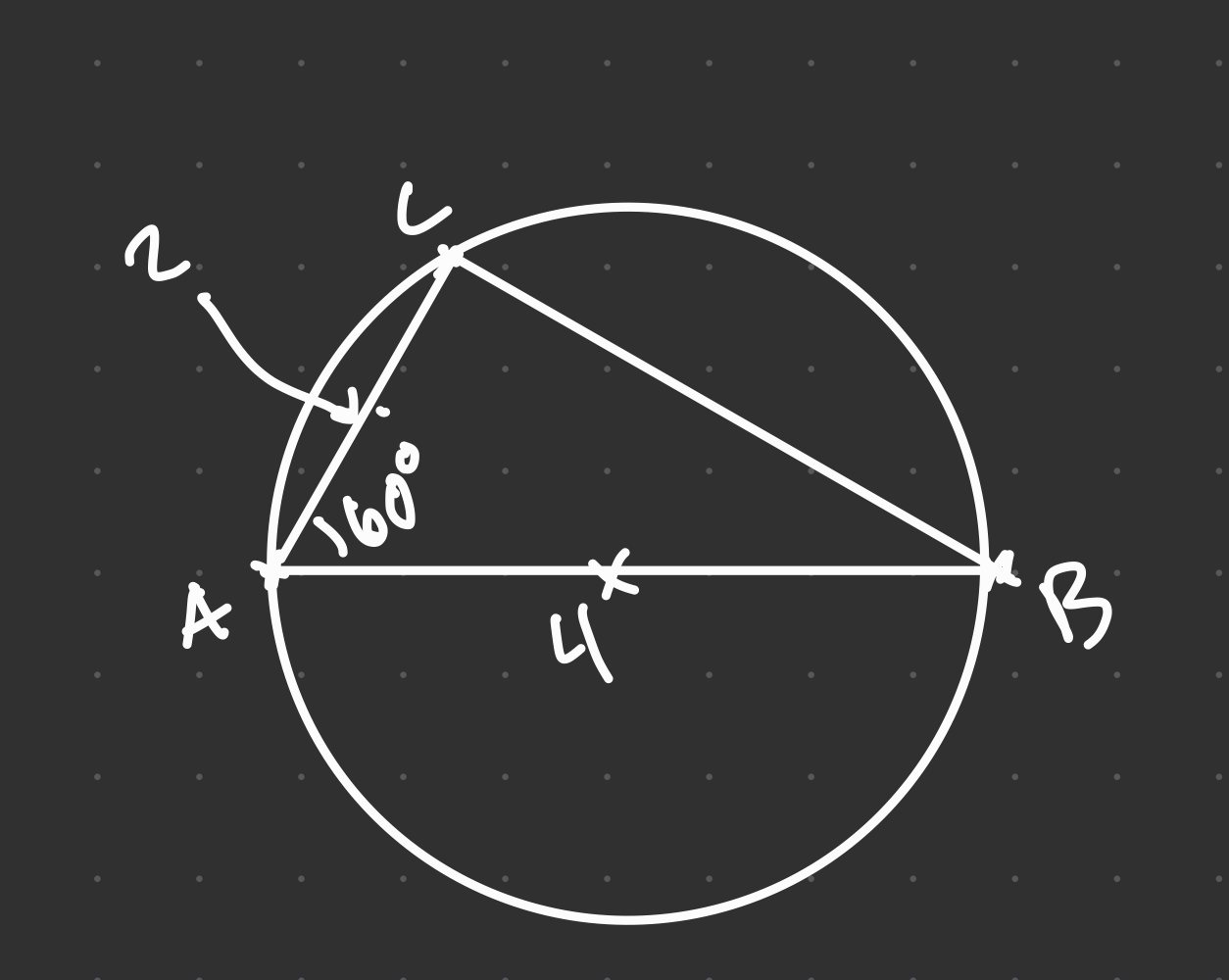Edit: Fixade hörnen. Punkten på AB är inte skalenlig heller.
Borde du inte kunna använda areasatsen?
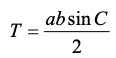
Ops jag läste inte att det var cirkelskivans area som du skulle beräkna, sorry :(
Det ska vara arean för cirkeln.
Triangeln ABC är "en halv liksidig triangel", så sidan AB är en diameter i cirkeln.
Hur drar du den slutsatsen? Eller vad menar du? Förstått att AB är en diameter, men inte varför.
Tillägg: 30 aug 2024 21:31
Jag har nu lyckats göra skalenliga figurer utan hjälpmedel, och där ser man att AB kan vara diametern, men skulle nog behöva något annat bevis för att den är just det.
Har testat förlänga AC med 2 och bildat en liksidig triangel. Förstår vad du menar med det nu men inte hur du går från det till att AB måste vara diametern i cirkeln.
Om en sida i en triangel är dubbelt så lång som en annan sida i samma triangel, och om den mellanliggande vinkeln ör 60 grader, så ÄR det en halv liksidig triangel. Strunta i cirkeln så länge och rita spegelbilden löngs den tredje sidan, så ser du adtt det blir en liksidig triangel.
Ja, det har jag gjort. Och det förstår jag (försökte lägga till det i mitt tillägg i inlägg #5). Det är delen med cirkeln som jag inte får in.
Randvinkelsatsen säger att en randvinkel är hälften så stor som medelpunktsvinkeln. Du har en vinkel som är 90 grader, låt den vara en randvinkel. Den längsta sidan i triangeln är båda benen i 180o-vinkeln.
Självklart. Jag hakade upp mig på vinkel C samt kollade på problemet på ett väldigt konstigt sätt. Tack för hjälpen.
