Area- & cosinussatsen - Bestäm area av fyrkant

Uppgiften lyder "En tomt har formen av en fyrhörning ABCD. Man utför följande mätningar: AB = 32m, BC = 24m, CD = 29m, A=87 $°$ och C = 98 $°$ . Vilken area har tomten?"

Jag har ritat denna bild för att visualisera det:

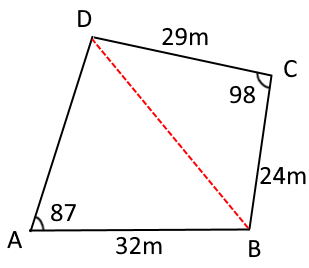
För att lösa denna tänkte jag att man först delar upp fyrkanten till 2 trianglar. Arean av BCD = $\frac{29 \times 24 \times \sin (98 °)}{2}$

Sen behöver vi ju arean av ABD men vi saknar AD. AD kan vi få ut genom cosinussatsen och observation att trianglarna delar sidan BD.

$A B D \to B D^{2} = A D^{2} + 32^{2} - 2 A D \times 32 \times \cos (87) B C D \to B D^{2} = 24^{2} + 29^{2} - 2 \times 29 \times 24 \times \cos (98)$

Vi ser att vänsterledet i båda ekvationerna är $B D^{2}$ vilket gör att vi kan sätta högerleden lika med varandra.

$A D^{2} + 32^{2} - 2 \times A D \times 32 \times \cos (87) = 24^{2} + 29^{2} - 2 \times 29 \times 24 \times \cos (98)$

Vi kan sedan lösa ut AD mha pq-formeln. Sen sätter vi in AD i areasatsen $\to \frac{A D \times 32 \times \sin (87)}{2}$

Och sen adderar vi de två areor vi fått. Dock känns detta lösningssätt rätt svårt med tanke på att man inte får använda miniräknare. Är det något jag gör fel eller finns det ett alternativt sätt att lösa uppgiften på?

Svaret i facit är $4 (87 \sin (98) + 104 \sin (87)) \approx 760 m^{2}$

När jag slår mitt svar i miniräknaren får jag att arean ABD antingen är -414 eller 360. Beroende på om AD har minus eller plus framför $\sqrt{. . .}$

Om jag använder 414 och adderar med arean av BCD får jag samma svar som facit men om jag använder 360 blir det fel.

Inte får använda miniräknare, hmm. Då blev en ganska rutinmässig uppgift litet mer utmanande. Får grubbla på den, återkommer.

Om man granskar facit ser man att uttrycket där inte är exakt. Räknar jag noga med din metod (jag hade inga problem med tecken) får jag svaret 759,325.

Räknar jag noga med facits uttryck får jag 760,043. Min misstanke är att facit gjort några avrundningar. Om så skulle vara, tycker jag inte det är riktigt hederligt; man förleds tro att

4(87sin(98)+104sin(87)) är ett exakt uttryck för arealen.

Värdena sin(98) och sin(87) är väl exakta, men var kommer faktorerna 87 och 104 från? Troligen är de avrundningar, men från vad? Får tänka litet till.

Nej, detta får någon smartskalle reda ut. Jag ser att AD ≈ 25,955. Om man avrundar det till 26 så ger areasatsen att triangeln ABD skulle ha arean 416 sin(87).

Arean av triangeln BCD är 348 sin(98)

Adderar vi dessa areor och bryter ut 4 får vi 4( 104sin(87) + 87sin(98)) dvs det facit anger.

Så jag har en stark förmodan att facit har använt värdet 26 för AD i stället för det exakta

32cos(87) + sqr[ 1024(cos²(87) –1) + BD² ] som alltså ≈ 25,955.

Men det löser inte frågan hur man utan räknare kommer fram till att AD är ungefär 26. Det finns såklart tabeller för sin och cos, men det tror jag inte är meningen.

Och det stör mig att svaret presenterar 4(87sin(98)+104sin(87)) på ett sätt som gör att man tror det är det exakta värdet utifrån figuren.

PS Man kan undra varför i fridens namn de inte mätte AD också när de ändå var igång med måttbandet.

Men OK, kan ha varit en bergknalle eller något i vägen.

Ja. Oavsett så är jag tacksam att ni la er tid att svara. Ex-tentorna jag gjort brukar ha "enkla" värden som skulle göra dessa uppgifterna lite lättare så får bara hoppas det blir så på tentan jag skriver också.

Svara

Visa senaste svar