Arctan ekvation
arctan((x-1)/(x+1))= arctanx + 3π/4

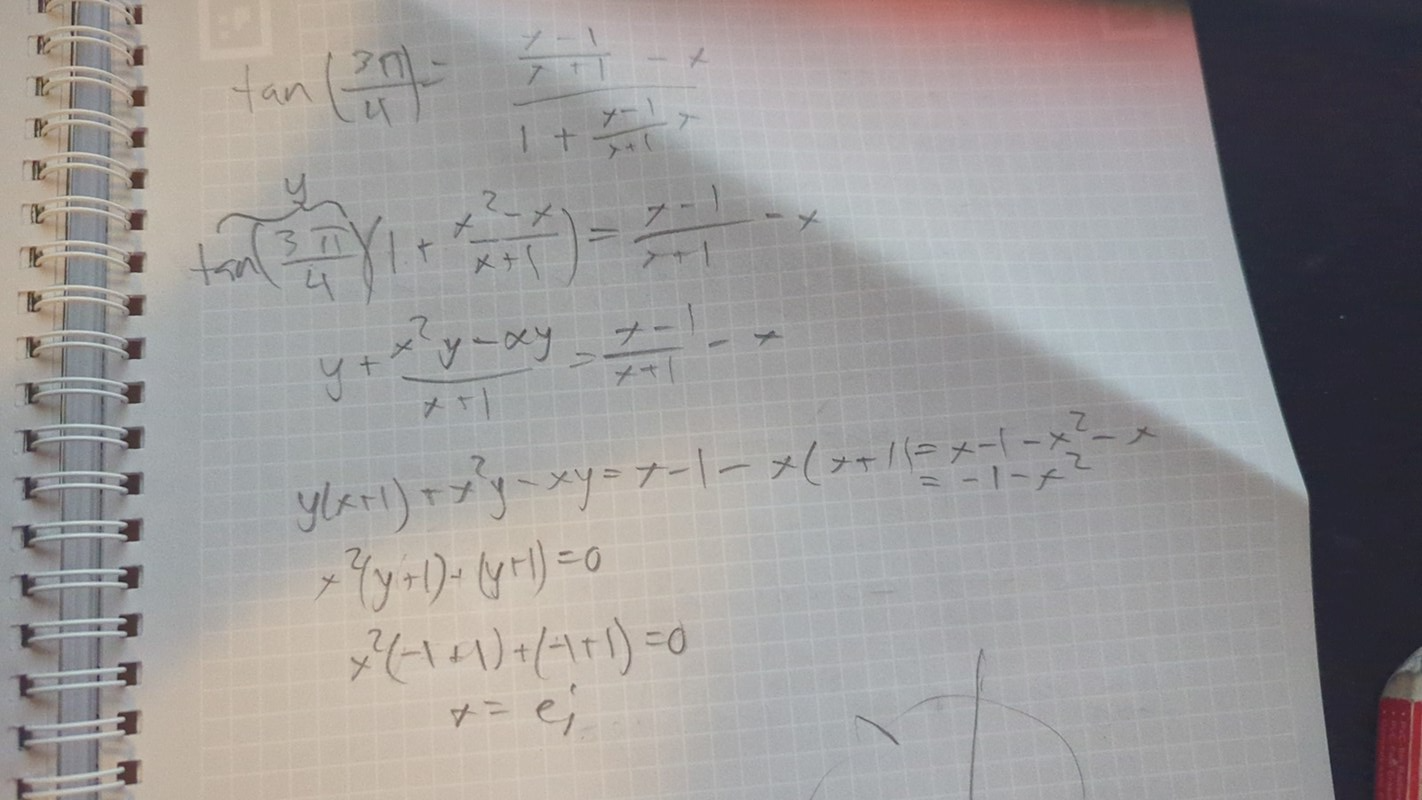
Bilder roterade. /MrP
Ta tan på båda leden och utnyttja formeln för tan(u+v) på H.L
Derivera båda led i andra raden och visa att funktionen är konstant för alla x.
Att sedan visa att det blir just den konstanten klarar du nog själv.
Men du borde oxå kika på funktionen i olika intervall eftersom den inte är kontinuerlig.
Tillägg: 26 sep 2024 07:39
Innan du deriverar!
Tillägg: 26 sep 2024 11:03
Den är kontinuerlig men du måste ändå kolla på intervallen större och mindre än 1!
Deriveringsmetoden ger inget svar
Hur får du fram att man ska kolla vid 1?
Och hur kollar jag intervallet utan räknare?
Om man använder ex geogebra så har de skärningspunkten x<-1
Jag menade -1. Det gör att man delar med 0 i bråket i arctan.
Om du deriverar bör du få fram att derivatan är 0 för alla x i Df. Därefter är det bara att ta vilket x som helst till vänster och höger om -1 så får du fram konstanterna i båda intervall.
Aha okej då fattar jag, låter rimligt. För jag fick ju 0 med derivatan så då tänkte jag att alla fungerade så jag testade x=0 men det funkar ju ej. Jag förstår varför det inte fungerar vid -1 men varför fungerar det x>-1?
Vad menar du med ej fungerar för x=0?
Om du ritar upp grafen ser du att den är konstant men konstanten är olika beroende på om x är större eller mindre än -1. Du ska svara det intervallet där konstanten är Pi/4.
Det jag mena är att det finns ingen skärningspunkt x>-1
Nää, det gäller då inte för något x. Om du skrivit uppgiften korrekt.
Svaret till uppgiften jag gav är x< -1 Så därför finns det ju inga skärningspunkter vid x>-1
Förstår ej. Där likheten stämmer ska grafen skära med 3Pi/4 i alla x i det intervallet.


