Är detta en godtagbar lösning?

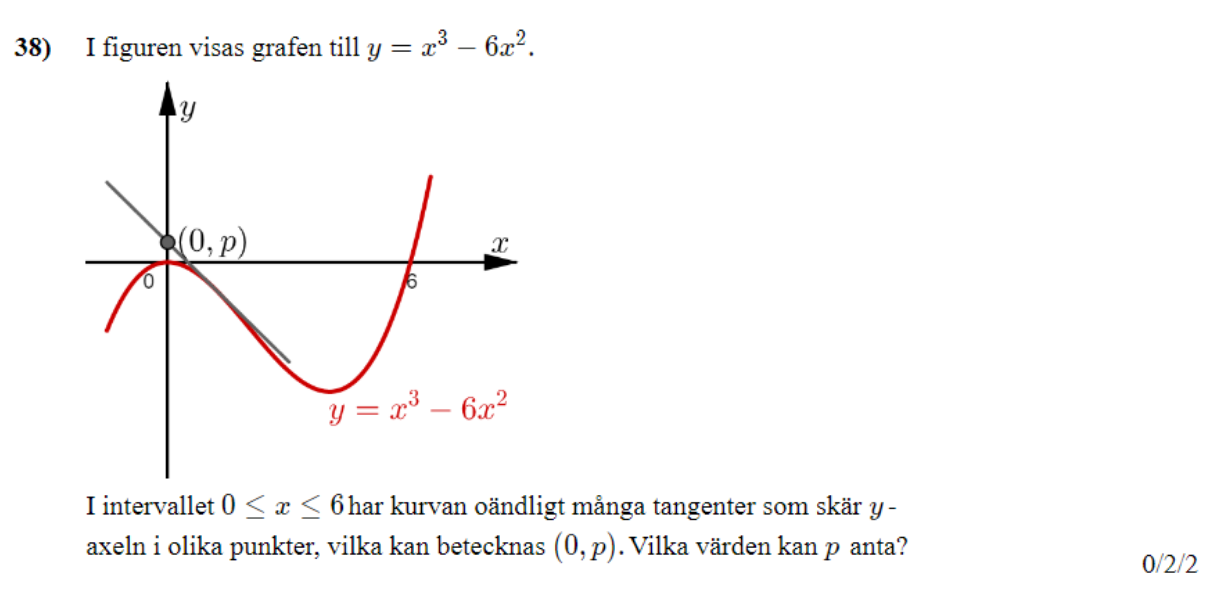
Låt tredjegradaren vara $f\left(x\right)$. Jag kan med hjälp av logiskt tänkande skriva upp följande samband:

$$\begin{gathered} f\left(x\right)=xf\text{'}\left(x\right)+p, för alla x \\ \Rightarrow p=f\left(x\right)-xf\text{'}\left(x\right) \\ \Rightarrow p=-2x^3+6x^2 \end{gathered}$$

Sedan är det bara att derivera funktionen p:

$p\text{'}=-6x^2+12x$

Vid en extrempunkt kommer

 $$\begin{gathered} p\text{'}=0 \\ \Rightarrow 12x=6x^2 \end{gathered}$$

Detta ger en lösningsmängd:

 $\left\{\begin{array}{l}x=0\\ x=2\end{array}\right.$

Sedan kan man verifiera med hjälp av andraderivata att just x=2 råkar vara en maximipunkt. Det är den enda maximipunkten funktionen har, och den ligger i intervallet [0, 6]. Därför erhåller man det största värdet på p vid x=2. Sedan gäller det att leta fram det minsta värdet på p. 

Vi vet att funktionen p är avtagande för alla x>2 (går att visa med derivata också). Med hjälp av detta kan vi säga att vi måste gå så långt ut i intervallet som möjligt för att erhålla det lägsta värdet på p. Då vet vi att detta värde erhålls vid x=6. 

Då gäller $-216\le p\le 8$.

Jag vet inte riktigt hur jag ska förklara hur jag kommer fram till funktionen p i mitt första steg. Jag bara "vet" att det är så, men jag vet inte riktigt hur jag ska förklara det. Måste jag förklara det? Jag är osäker på om "jag tänkte logiskt" håller vid bedömning.