Är dessa två ekvationer likadana?

Det står c₁ på ena stället och c på andra stället. Om dessa två är lika så är lösningarna olika.

Kan du ladda upp en bild på uppgiften och din lösning?

det är uppgift 4021 b. Tror dock inte det är någon skillnad mellan C:na. 

kan ersättas med "K" , en konstant. Jag vet ej vilken relevans c_1 eller 100c_1 har till problemet.

Olika K ger olika lösningskurvor

Allting stämmer överens med facit förutom termen med c. C och C₁ verkar vara samma sak, enligt läraren. Hjälper det att besvara frågan?

Hejsan266 skrev:

Allting stämmer överens med facit förutom termen med c. C och C₁ verkar vara samma sak, enligt läraren. Hjälper det att besvara frågan?

Nej

100c = e^(100c_1). Det kan vara att facit glömt "e^" framför. I vilket fall som helst är det inget bra svar då man inte har relaterat c till något begynnelsevärde eller likn. En konstant K är ett bättre val.

Om du skulle lösa uppgiften med digitala hjälpmedel, hur skulle du göra då?

Hejsan266 skrev:

Om du skulle lösa uppgiften med digitala hjälpmedel, hur skulle du göra då?

Menar du grafräknare? Den 'enklare' typen av hjälpmedel kan jag inte längre. Jag anv. aldrig dessa och de har så olika syntax beroende på om det är Casio eller Texas Inst eller HP.

Om man bara skall lösa den med "vilken kraft du än finner på nätet" hade jag gjort som du gjort i #2. Man kan inte göra så mycket mer, konstanten går ej att bestämma. Jag vet ej varför Wolfram svarar på det formatet och inte bara "c_1". Det kan vara så att c_1 ramlar ut ur någon inre procedur och sedan följer det med ut hela vägen genom flertalet aritmetiska operationer

Det ser inte mycket bättre ut i Mathematica

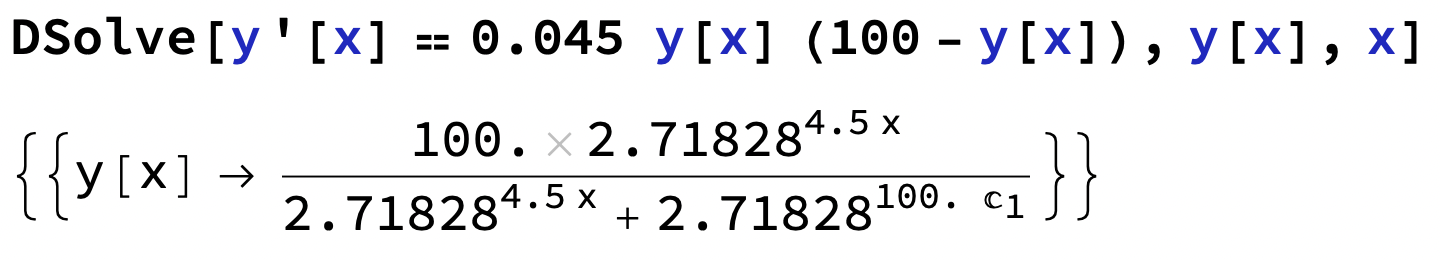
men det blir 'snyggare' om vi räknar exakt (0.045 rör till det för Mathematica...)

Kör vi FullSimpify på det får vi en annat format, men fortfarande med en besynnerlig konstant 50c_1

Dock ser man gränsvärdet då x->oo lättare på kvotformen.

Man får manuellt tvinga den till "bättre matematiskt vetande"

Möjligtvis svarar den på den tidigare formen för att få ett "snyggt" svar om man känner y(x_0)=y_0

Bryter man sedan ut e^(9x_0/2) får man en snygg kvot (100-y_0)/y_0 och tillämpar man logaritmlag på den utbrutna faktorn blir man av med e och då kommer 0.045 tillbaka igen dår 1/100*9/2=0.045. Jag vet ej om Mathematica är så 'slug' och motiverar sitt svar på detta sätt. Tveksamt, men man vet aldrig.

Det ser nästan ut som att vi har samma svar. Kan jag tolka mitt svar som rätt även om facit har något annat?

Ja, ditt svar är lika rätt som något annat av de olika formaten. Så länge vi ej vet mer om situationen finns det inget som säger att något svar är bättre än det andra. Du kan du anmärka i din text att "tack vare" 0.045 så kommer W.A. att ej få rätt på e utan använder 2.71... Gör om samma beräkning med 45/1000 och se vilket svar du får då. Gör denna observation som en N.B. sist i din text.

Du kan du anmärka i din text att "tack vare" 0.045 så kommer W.A. att ej få rätt på e utan använder 2.71... Gör om samma beräkning med 45/1000 och se vilket svar du får då. Gör denna observation som en N.B. sist i din text.

Kan inte dessa förkortningar. Så felet är att e nu är 2,71 istället för 2,72?

Hejsan266 skrev:

Du kan du anmärka i din text att "tack vare" 0.045 så kommer W.A. att ej få rätt på e utan använder 2.71... Gör om samma beräkning med 45/1000 och se vilket svar du får då. Gör denna observation som en N.B. sist i din text.

Kan inte dessa förkortningar. Så felet är att e nu är 2,71 istället för 2,72?

"2.7...." i

skall vara e.

N.B. = nota bene

https://en.wikipedia.org/wiki/Nota_bene

Det ser 'fint' ut att avsluta en text med detta där man markerar att 0.045 är inexakt för Wolfram medans 45/1000 ger ett mera korrekt svar.