Är denna naturliga deduktionen rätt?
Uppgift:
![]()
Min lösning:
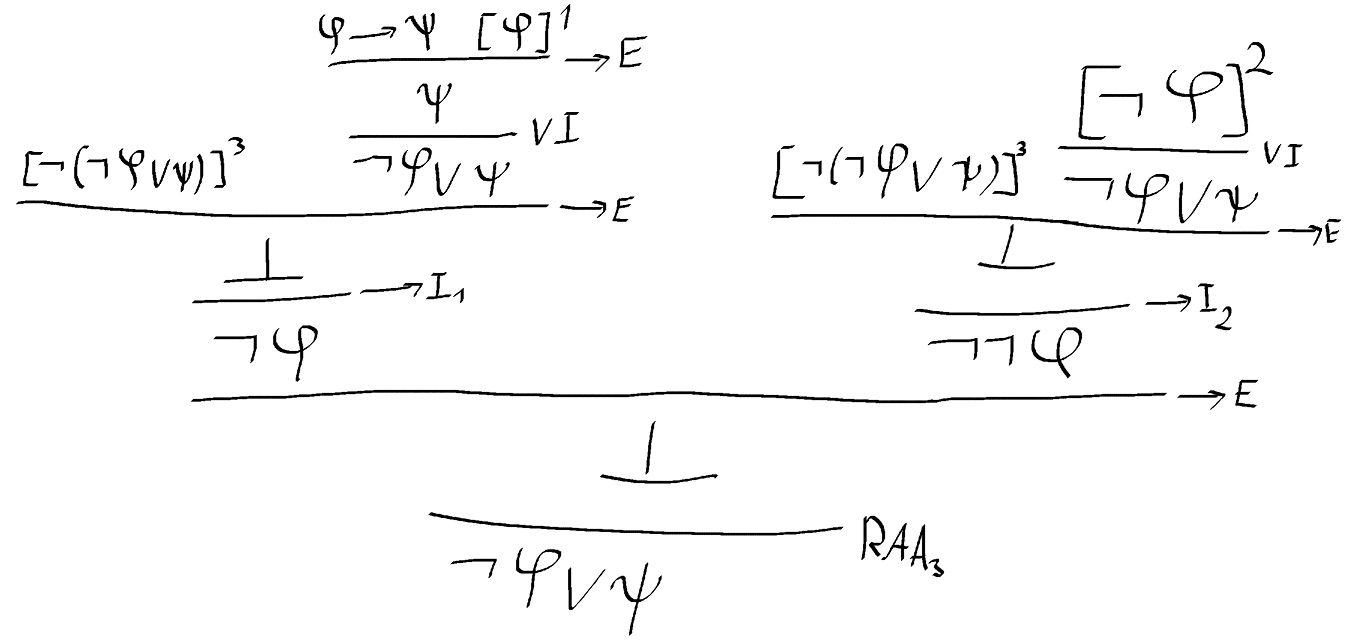
Facit:
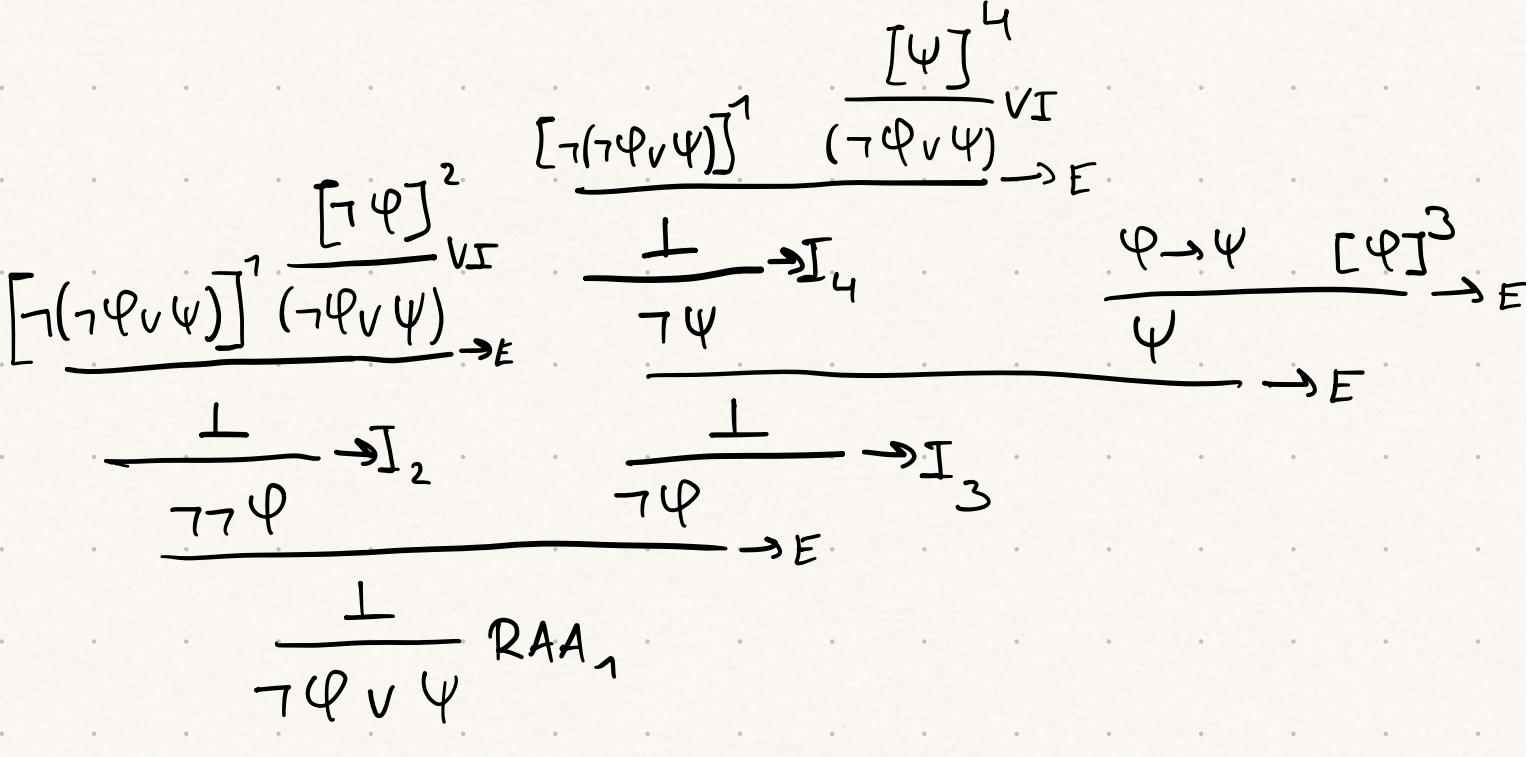
Jag kan inte se några fel med min lösning men lösningen i facit är helt annorlunda. Är min lösning rätt?
Förlåt att jag inte kan hjälpa, men vad pluggar du där såna här frågor dyker upp? Jag har pluggat matematik på rätt hög nivå, men detta är grekiska för mig. Bokstavligen grekiska, hehe.
Ämnet kallas "Matematisk logic". Det ser nog svårare ut än vad det faktiskt är. Uppgiften säger att man ska kunna dra slutsatsen "(inte ) eller " från antagandet " implicerar ". och representerar vanliga menigar som antingen är sanna eller falska, till exempel "det regnar ute "eller "50 är mer än 100". I detta fall skulle den första meningen vara sann om det regnar ute och falsk om det inte regnar men den andra meningen är alltid falsk hur man än tolkar den.
Ok, jag förstår helt och hållet. Jag stött på lite sånt tidigare, men aldrig till denna nivå. Får jag fråga vad du pluggar där sånt här dyker upp? Någon slags kandidat i matematik?
Jag googlade runt lite lätt på deduktion och första resultatet som kom fram var "logik för dataloger", vilket skrämde mig, då jag själv är datalog.
Jag studerar fristående kurser där målet är en kandidat examen i matematik. Det är nog några i logik kursen som studerar datalogi.
Logik för dataloger borde inte vara så djup, tycker jag, om det inte är just en teorembevisare man ska skriva.
Logik är ett gammalt ämne, och brukade och brukar kanske fortfarande ligga under filosofi och inte matematik, även när det behandlas väldigt stringent.
Ett levande forskningsområde är bevissystem och hur mycket man kan bevisa om man använder andra axiom än naturlig deduktion men naturlig deduktion är nog det första man lär sig i en kurs om logik.
Det finns också modal logik, temporal logik, linjär logik och en massa andra, antingen begränsade på något sätt eller utökade med nya operatorer.
SkogN skrev:Jag studerar fristående kurser där målet är en kandidat examen i matematik. Det är nog några i logik kursen som studerar datalogi.
Najs! Tack för info!
Laguna skrev:Logik för dataloger borde inte vara så djup, tycker jag, om det inte är just en teorembevisare man ska skriva.
Logik är ett gammalt ämne, och brukade och brukar kanske fortfarande ligga under filosofi och inte matematik, även när det behandlas väldigt stringent.
Ett levande forskningsområde är bevissystem och hur mycket man kan bevisa om man använder andra axiom än naturlig deduktion men naturlig deduktion är nog det första man lär sig i en kurs om logik.
Det finns också modal logik, temporal logik, linjär logik och en massa andra, antingen begränsade på något sätt eller utökade med nya operatorer.
Jag hoppas att du har rätt med att logiken blir ytlig för mig! Gillar inte konceptet av detta särskilt mycket. Sedan suger min skrivstil, så detta skulle inte passa mig.
Dock har jag inte sett något om logik i min kursplan, så jag kanske slipper;
Läste också matematisk logik men skulle lösa detta med att skriva sanningstabeller för vardera sidan och se att de blir lika. Känner inte igen bevisnotationen.


