Min lösning med hjälp av Geogebra: facit säger 16,3 l.e men jag fick 16,3, vilket är väldigt nära. finns det andra metoder?
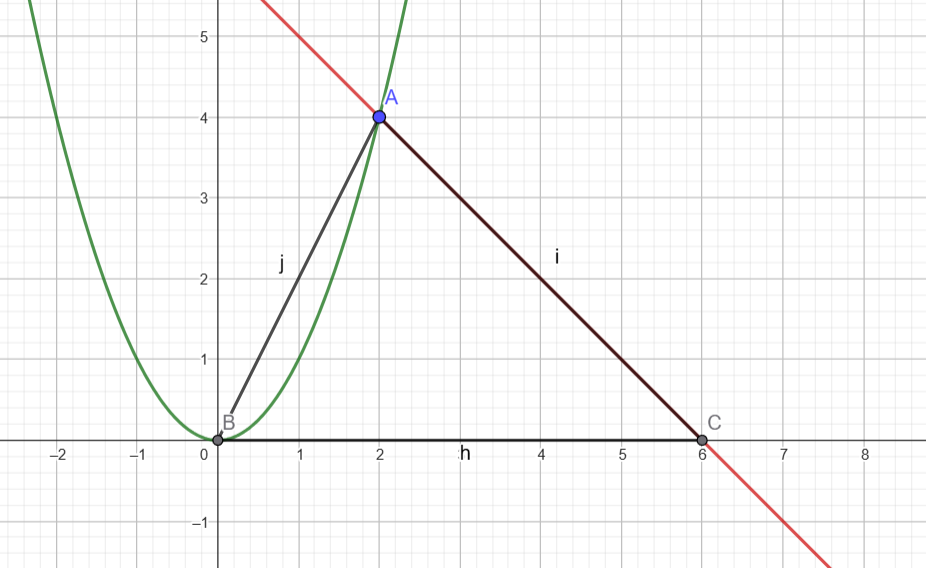
Tanken är att du ska använda dig av formeln som ges i frågan. Att endast dra en rät linje mellan A och B kommer ge en annan omkrets som skiljer sig från det rätta svaret. Även om det avrundas och ger samma resultat så har du inte beräknat omkretsen på det sätt som frågar vill.
Testa att använda formeln i uppgiften och se hur långt du kommer!

Tillägg: 8 apr 2025 21:57
Så lång jag har kommit, men det känns fel. När jag deriverar funktionen y = 6 - x får jag bara en konstant, då jag kan inte beräkna f'(6).
Du ska inte stoppa in några siffror i själva integranden. Det ska alltså inte stå f'(2) utan enbart f'(x). Sen gör du det lite klurigare för dig själv. Behöver formeln verkligen användas för alla delar? Mellan A och C och B och C är det ju bara raka linjer. Då kan du använda avståndsformeln för att få fram de sträckorna. Sen kan du använda formeln i uppgfiften för den böjda linjen mellan A och B.
AMGOP skrev:
Tillägg: 8 apr 2025 21:57
Så lång jag har kommit, men det känns fel. När jag deriverar funktionen y = 6 - x får jag bara en konstant, då jag kan inte beräkna f'(6).
Om derivatan är konstant innebär det ju bara att den har samma värde för alla värden på x. Vilket är skönt, då slipper man ju utföra beräkningar!
men hur jag göra nu (:
Lösningsförslag
Visa spoiler

Trinity2 skrev:Lösningsförslag
Visa spoiler
Halv kvadrat? Hur fick du fram? Jag förstod inte riktigt ):
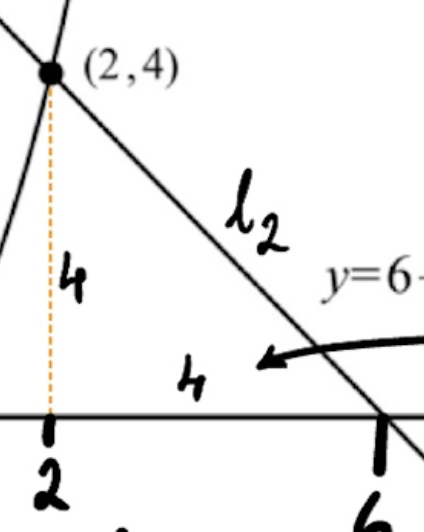
Längs x-axel: 2 och 6, det ger 6-2=4 i basen på triangeln
Höjden är 4 då punkten är (2,4).
En triangel med lika sidor i rät vinkel är en halv kvadrat.
Du kan även använda Pythagoras' sats om du vill
l2^2 = 4^2+4^2
.....