Använder jag rätt/fungerande metod? Induktionsbevis.
Hej! Jag undrar om jag gör rätt, eftersom bokens facit lösning ser annorlunda ut men vi båda kommer fram till samma sak. Är min metod tydligare eller inte? Jag fattar inte heller längst ner på facitens lösning på pappret, varför det står (enligt antagandet) just där? Vadå enligt antagandet? Jag brukar aldrig se de skriva sådär på andra uträkningar.
Uppgiften:
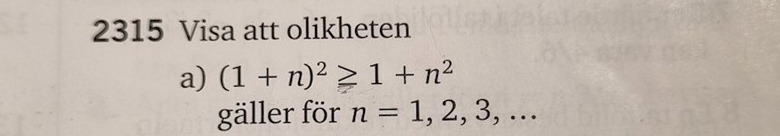
Facit:

Min uträkning:
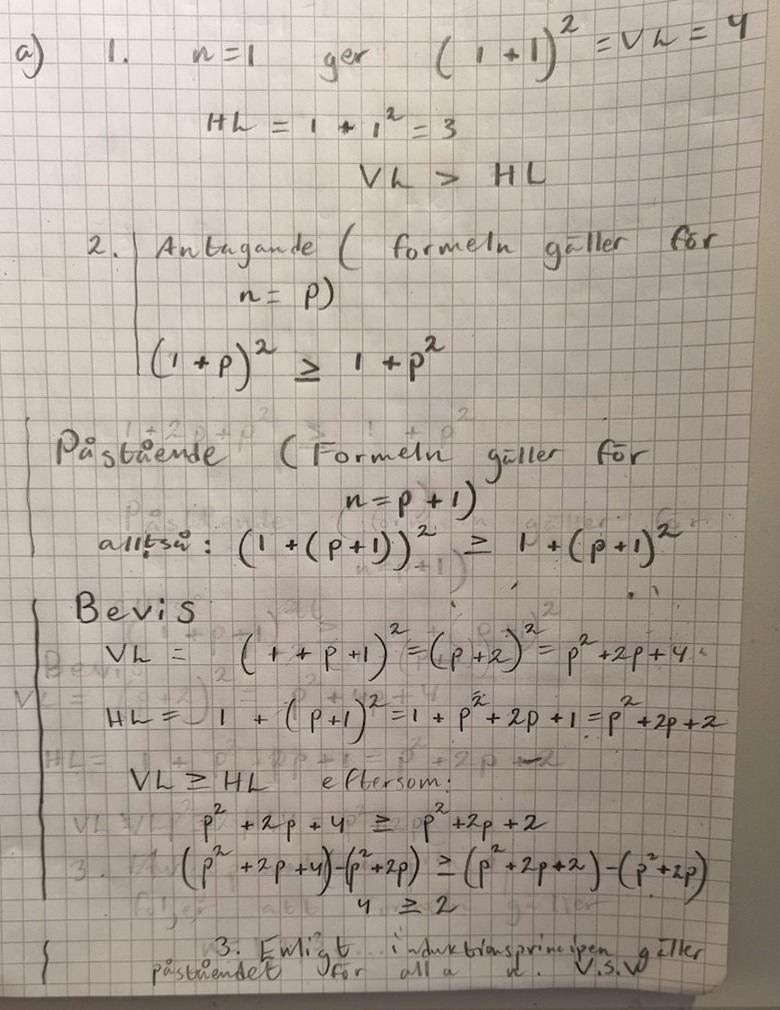
Personligen tycker jag detta är en rätt så dålig uppgift för att bevisa med induktion. Tycker inte om uppgiften eller facit.
. Detta är klart större än då vi bara har tagit bort det positiva talet .
Beviset du skrev är ett korrekt bevis för påståendet men inte med induktion, eftersom antagandet inte används.
Iden med induktion är att man ska visa att om påståendet gäller för något heltal så gäller det för . Då antar vi att det gäller för och visar att det medför att påståendet stämmer för . Det är det de menar med "enligt antagandet". De använder antagandet att påståendet stämmer för för att bevisa att det då också stämmer för .
Såhär tänker jag att ett bevis med induktion för detta ska se ut, jag hoppar över basfallet.
Om vi antar att för talet gäller det att
Nu ska vi visa att det i så fall gäller för . Alltså ska vi visa att
. Nu kan vi använda antagandet. Vi har ju antagit att . Alltså är
Det här kan vi förenkla: och då är påståendet bevisat.
Att bevisa ett sådant här påstående med induktion är lite knöligt. Bättre induktionsbevis för olikheter är exempelvis: Visa att om
AlexMu skrev:Personligen tycker jag detta är en rätt så dålig uppgift för att bevisa med induktion. Tycker inte om uppgiften eller facit.
. Detta är klart större än då vi bara har tagit bort det positiva talet .Beviset du skrev är ett korrekt bevis för påståendet men inte med induktion, eftersom antagandet inte används.
Iden med induktion är att man ska visa att om påståendet gäller för något heltal så gäller det för . Då antar vi att det gäller för och visar att det medför att påståendet stämmer för . Det är det de menar med "enligt antagandet". De använder antagandet att påståendet stämmer för för att bevisa att det då också stämmer för .
Såhär tänker jag att ett bevis med induktion för detta ska se ut, jag hoppar över basfallet.
Om vi antar att för talet gäller det att
Nu ska vi visa att det i så fall gäller för . Alltså ska vi visa att
. Nu kan vi använda antagandet. Vi har ju antagit att . Alltså är
Det här kan vi förenkla: och då är påståendet bevisat.
Att bevisa ett sådant här påstående med induktion är lite knöligt. Bättre induktionsbevis för olikheter är exempelvis: Visa att om
Vad sker på slutet? Gjorde du tvärtom på HL och VL? Och vad sker vid förenklingen?
Studenten06 skrev:AlexMu skrev:Personligen tycker jag detta är en rätt så dålig uppgift för att bevisa med induktion. Tycker inte om uppgiften eller facit.
. Detta är klart större än då vi bara har tagit bort det positiva talet .Beviset du skrev är ett korrekt bevis för påståendet men inte med induktion, eftersom antagandet inte används.
Iden med induktion är att man ska visa att om påståendet gäller för något heltal så gäller det för . Då antar vi att det gäller för och visar att det medför att påståendet stämmer för . Det är det de menar med "enligt antagandet". De använder antagandet att påståendet stämmer för för att bevisa att det då också stämmer för .
Såhär tänker jag att ett bevis med induktion för detta ska se ut, jag hoppar över basfallet.
Om vi antar att för talet gäller det att
Nu ska vi visa att det i så fall gäller för . Alltså ska vi visa att
. Nu kan vi använda antagandet. Vi har ju antagit att . Alltså är
Det här kan vi förenkla: och då är påståendet bevisat.
Att bevisa ett sådant här påstående med induktion är lite knöligt. Bättre induktionsbevis för olikheter är exempelvis: Visa att omVad sker på slutet? Gjorde du tvärtom på HL och VL? Och vad sker vid förenklingen?
Jag skrev det nog lite otydligt. Jag började med HL och sedan skrev jag om uttrycket för att använda induktionsantagandet och tillslut fick jag fram VL. De flesta förenklingarna var att faktorisera eftersom det är lika med
På röd markerade, menar de att (1+p)^2 = 1 +p^2 ? Är det från antagandet? Då har jag fattat hur man gör. Man ska använda antagandets för att kunna visa att den är större?
Studenten06 skrev:På röd markerade, menar de att (1+p)^2 = 1 +p^2 ? Är det från antagandet? Då har jag fattat hur man gör. Man ska använda antagandets för att kunna visa att den är större?
Antar att du menar ett större än eller lika med tecken, inte lika med. Men ja, poängen med induktion är att man använder antagelsen för att visa att påståendet stämmer för nästa tal. Ett annat exempel som jag personligen tycker är mer konkret är frågan:
Bevisa att
om
Då kan vi börja med basfallet
, . Påståendet stämmer.
För induktionsantagandet antar vi att för talet stämmer det att
För fallet ska vi visa att
. Men eftersom vi vet att från induktionsantagandet kan vi använda det för att skapa en olikhet.
Alltså är . Sedan kan man avsluta beviset genom att visa att , men detta är ett exempel på hur man använder induktionsantagandet



