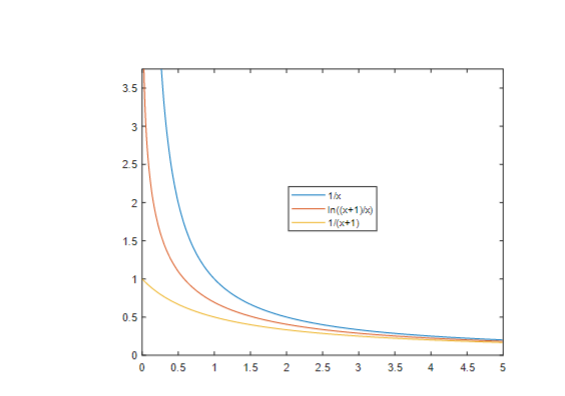
Använd olikheten för att beräkna gränsvärdet
Hej! Jag har en fråga vad gäller lösningen till ug. b) på 5:e bilden nedan förstår jag inte hur de tänkt och hur de får fram att
(ln (x+ 1) - ln x)/ 1 =( f(x+ 1) - f(x))/( (x+ 1) - x) = f`(c) = 1/c?
täljaren förstår jag att (ln (x+ 1) - ln x) =( f(x+ 1) - f(x))
men hur vet de att det ska vara 1 i nämnaren i vänsterledet? och hur vet de att allt detta är lika med 1/c?
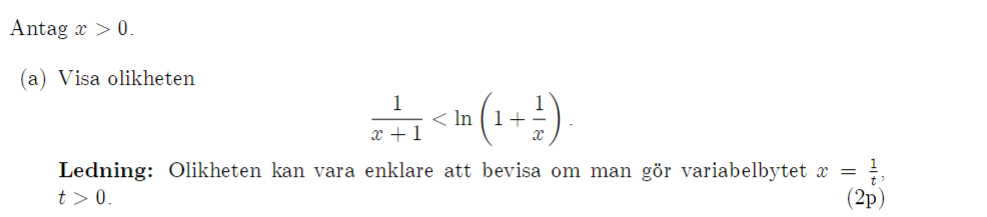
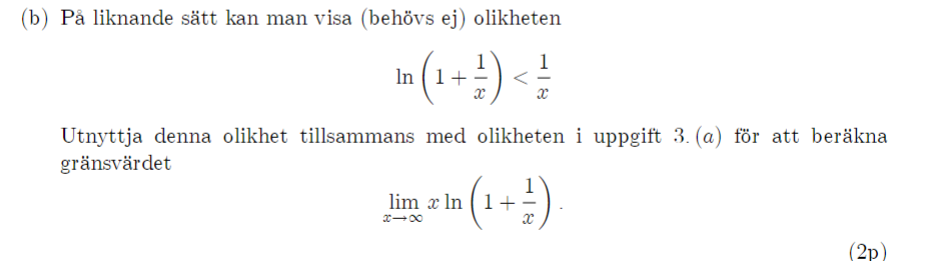
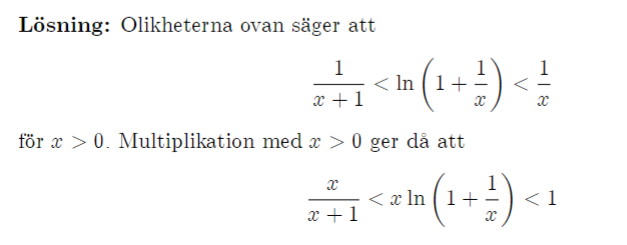

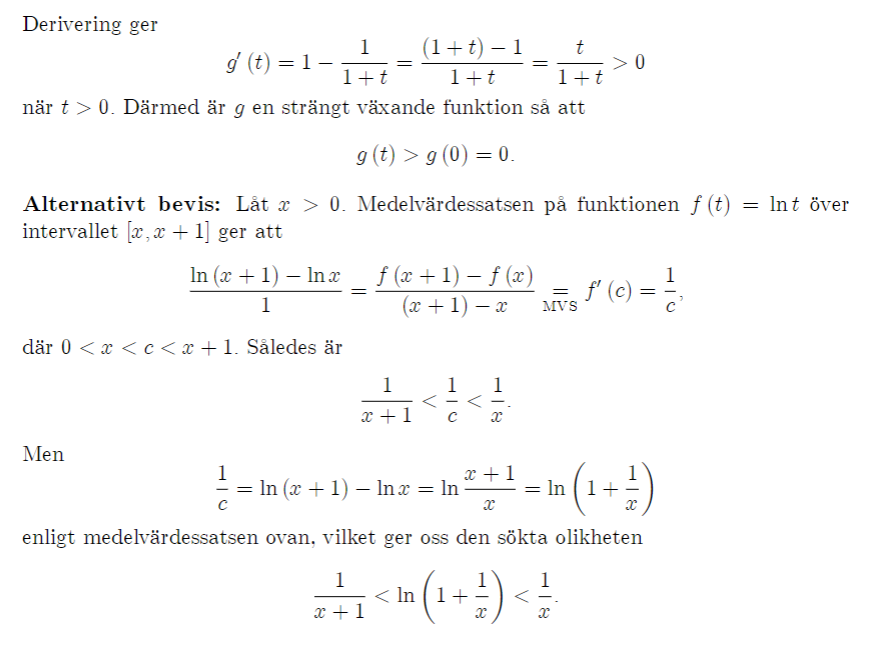
Tack på förhand!
Mvh Johanna
Det är helt enkelt vad Medelvärdessatsen säger: "Om en funktion f(x) är kontinuerlig på det slutna intervallet [a,b] och deriverbar på det öppna intervallet (a,b), så finns en punkt c i (a,b) sådan att f(b) - f(a) = f'(c)(b-a)."
Vi tar intervallet [x,x+1].
a = x, b=x+1
Så blir (b-a) = 1. Och enligt Medelvärdessatsen måste det finnas minst en sådan c mellan x och x+1. (någonstans)
Ah okej då tror jag jag förstår tack! Så f`(c) = 1/c då f = lnx och f`(x) = 1 /x?
Ja.

