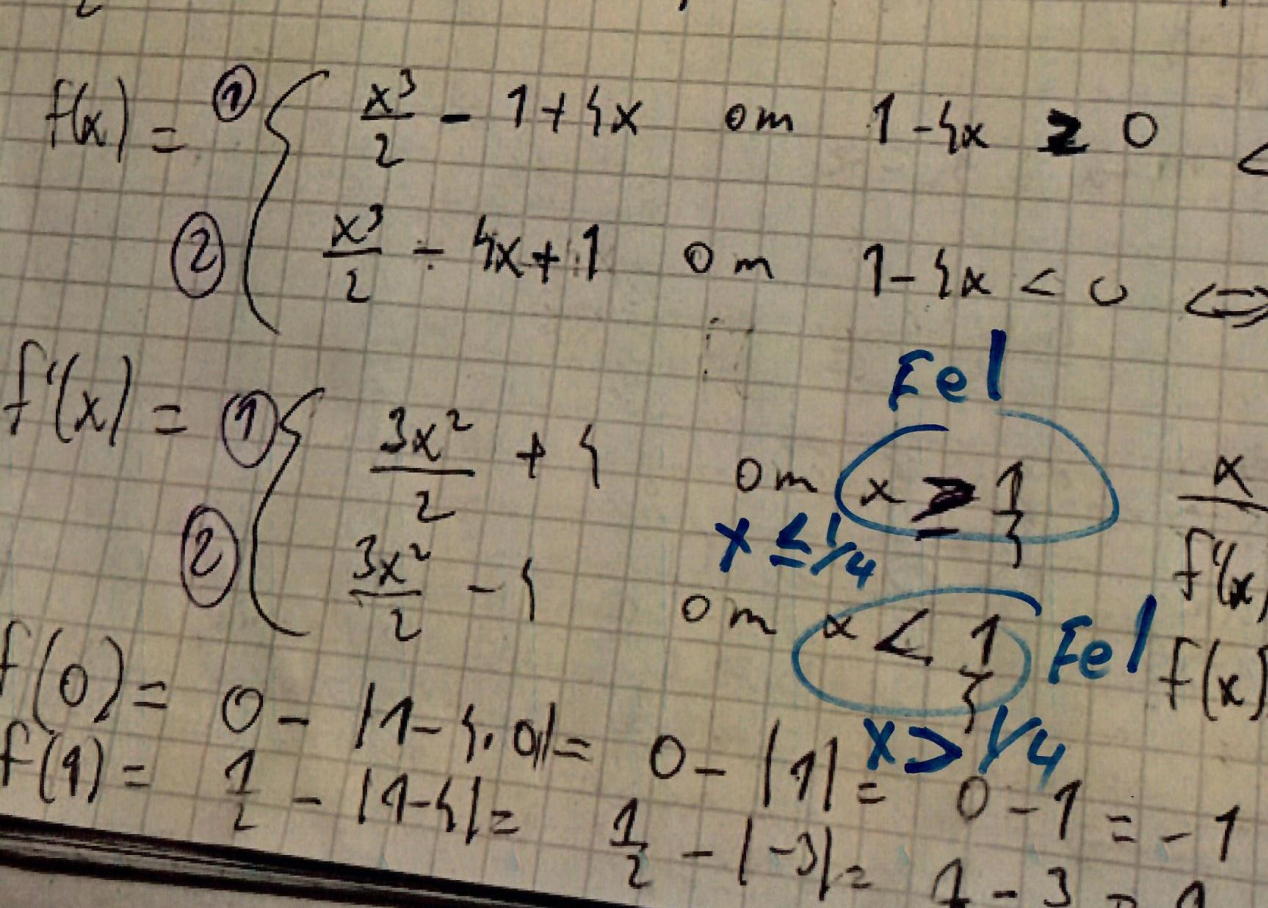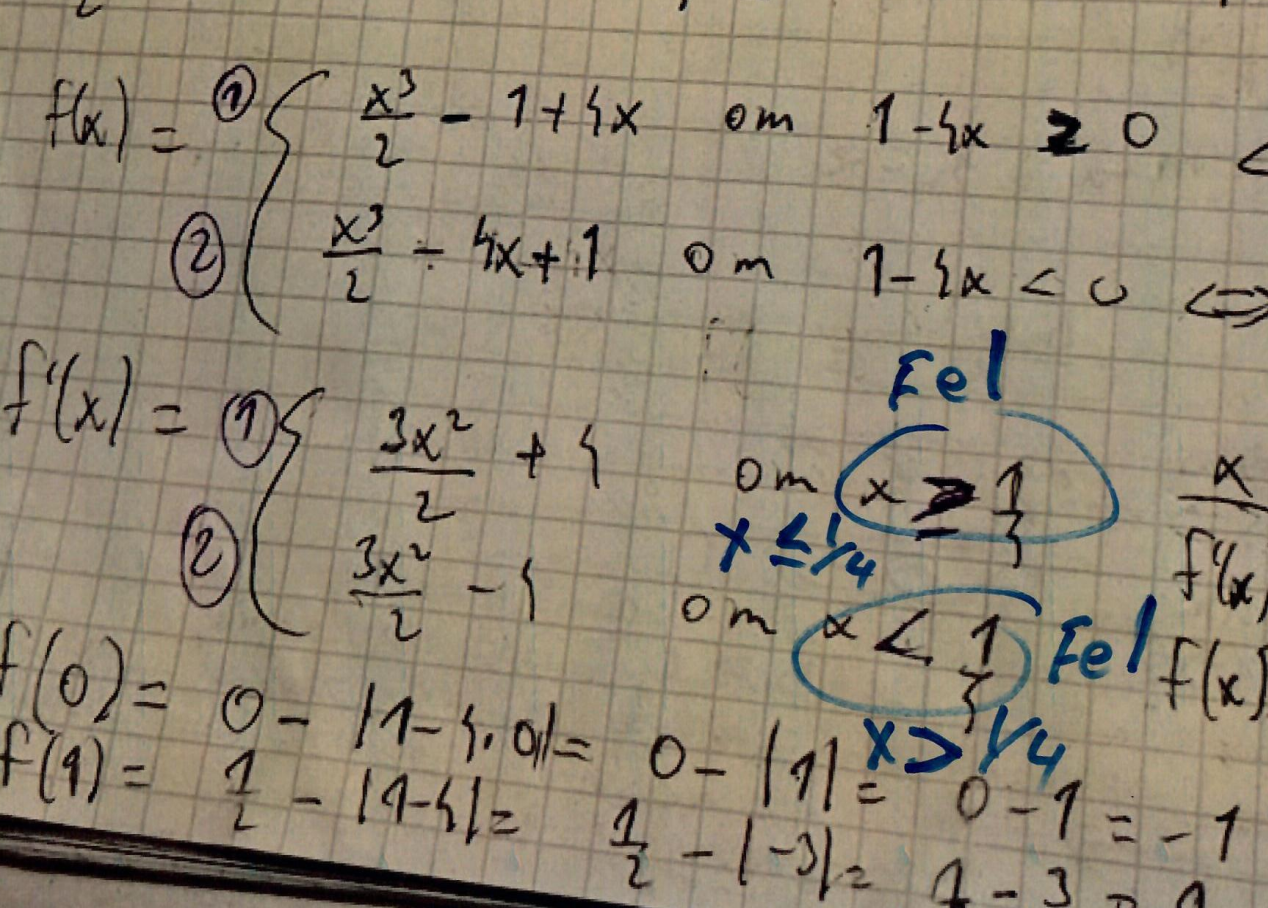Antal lokal maxima/minima
Hej!
Varför är mitt svar fel? Båda funktionerna saknar derivatans nollställe ju.


funktionen kan ha lokala extrempunkter där den inte är deriverbar
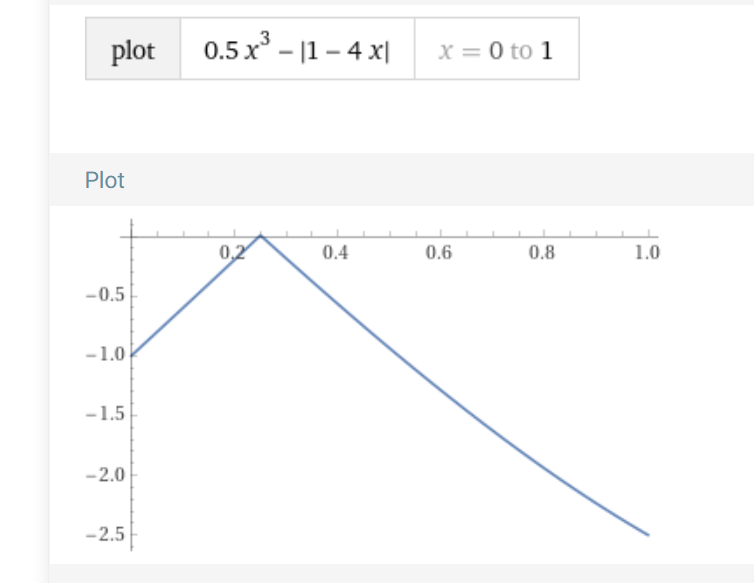
så här ser funktionen ut i intervallet 0 till 1
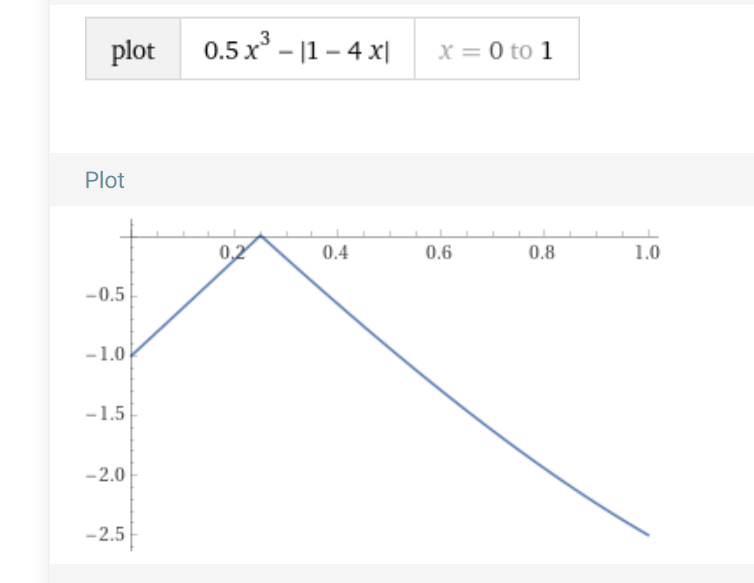
Ture skrev:funktionen kan ha lokala extrempunkter där den inte är deriverbar
så här ser funktionen ut i intervallet 0 till 1
Så du menar att vi ska stoppa in 0 och 1 i derivatan eller vad ska man göra? Jag har gjort teckentabell och hittade att x=1/4 är en lokal min. Sen påstår sidan att jag har felaktiga största o minsta värde..
sätt in x = 0,25 så upptäcker du att y > än f(0) och f(1)
Alltså finns det ett lokalt max
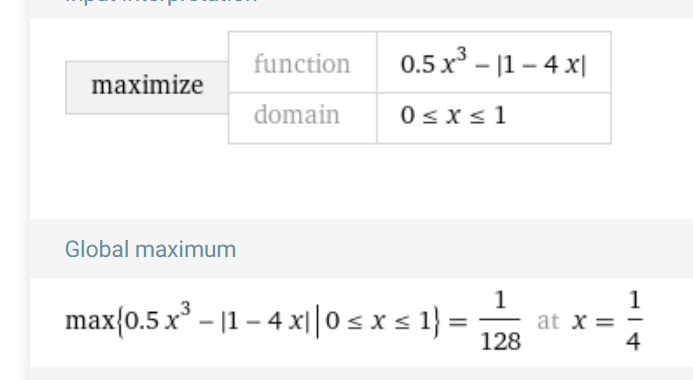
Minsta värde -2,5 för x = 1
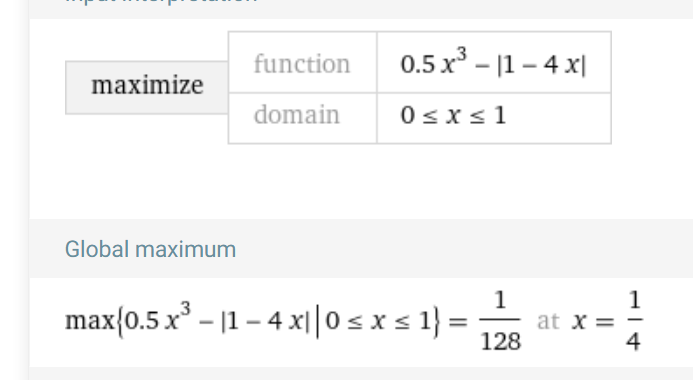
största värde 1/128 för x = 0,25
Ture skrev:sätt in x = 0,25 så upptäcker du att y > än f(0) och f(1)
Alltså finns det ett lokalt max
Minsta värde -2,5 för x = 1
största värde 1/128 för x = 0,25
Nu fick jag rätt gällande största och minsta värde. Enda vi behöver korrigera är antal lokala maxima och lokala minima som ej existerar enligt mig
Jag påstår att det finns ett lokalt max, men inget lokalt min
Absolutbelopp är luriga!
Eftersom funktionen är kontinuerlig i hela intervallet (även om den inte är deriverbar överallt) och det finns funktionsvärden som är större än definitionsgränsernas funktionsvärden så finns det ett lokalt max.
Ture skrev:Jag påstår att det finns ett lokalt max, men inget lokalt min
Absolutbelopp är luriga!
Eftersom funktionen är kontinuerlig i hela intervallet (även om den inte är deriverbar överallt) och det finns funktionsvärden som är större än definitionsgränsernas funktionsvärden så finns det ett lokalt max.
Det är ej vad jag får i teckentabell studie. Jag får att x=1/4 är en lokal min. Vad gör jag för fel tror du?
Jag tror du har förväxlat dina två derivator, den första raden är väl om x är mindre än 1/4?
Ture skrev:Jag tror du har förväxlat dina två derivator, den första raden är väl om x är mindre än 1/4?
Jag har 2 derivator. Se bild nedan. Vad har jag förväxlat?

Den första gäller för x mindre än 1/4
Den undre för x större än 1/4.
Du har skrivit tvärtom
Ture skrev:Den första gäller för x mindre än 1/4
Den undre för x större än 1/4.
Du har skrivit tvärtom
Asså det är |1-4x| om x>=1/4 så är det ju 1-4x första fallet men eftersom minus framför uttrycket 1-4x så får vi -1+4x. Andra fallet då x<1/4 så får vi -1+4x. Men eftersom det står ett minus tecken framför uttrycket så blir 1-4x. Se bild
Se bild nedan.

ja men du gör fel,
f(x) = x3/2 -1+4x om 1-4x >= 0, OK!?
då blir f'(x) = 3x2/2 +4, om 1-4x >= 0
Nu kollar vi på uttrycket
1-4x >= 0
addera 4x i bägge led
1 >= 4x
dela med 4
1/4 >= x vilket är samma sak som
x <= 1/4
Men du skriver tvärtom (x >= 1/4)
Ture skrev:ja men du gör fel,
f(x) = x3/2 -1+4x om 1-4x >= 0, OK!?
då blir f'(x) = 3x2/2 +4, om 1-4x >= 0
Nu kollar vi på uttrycket
1-4x >= 0addera 4x i bägge led
1 >= 4x
dela med 4
1/4 >= x vilket är samma sak som
x <= 1/4Men du skriver tvärtom (x >= 1/4)
Ja så skrev vår föreläsare. Jag bara imiterade sättet
destiny99 skrev:Ture skrev:ja men du gör fel,
f(x) = x3/2 -1+4x om 1-4x >= 0, OK!?
då blir f'(x) = 3x2/2 +4, om 1-4x >= 0
Nu kollar vi på uttrycket
1-4x >= 0addera 4x i bägge led
1 >= 4x
dela med 4
1/4 >= x vilket är samma sak som
x <= 1/4Men du skriver tvärtom (x >= 1/4)
Ja så skrev vår föreläsare. Jag bara imiterade sättet
Du skrev det här:
f(x) = x3/2 -1+4x om 1-4x >= 0,
Vilket är rätt
Sen deriverade du det och fick
f'(x) 3x2/2 +4, vilket är rätt, efter det skrev du att det gäller för x >= 1/4 vilket är fel, som jag visade i mitt förra inlägg
Ture skrev:destiny99 skrev:Ture skrev:ja men du gör fel,
f(x) = x3/2 -1+4x om 1-4x >= 0, OK!?
då blir f'(x) = 3x2/2 +4, om 1-4x >= 0
Nu kollar vi på uttrycket
1-4x >= 0addera 4x i bägge led
1 >= 4x
dela med 4
1/4 >= x vilket är samma sak som
x <= 1/4Men du skriver tvärtom (x >= 1/4)
Ja så skrev vår föreläsare. Jag bara imiterade sättet
Du skrev det här:
f(x) = x3/2 -1+4x om 1-4x >= 0,
Vilket är rätt
Sen deriverade du det och fick
f'(x) 3x2/2 +4, vilket är rätt, efter det skrev du att det gäller för x >= 1/4 vilket är fel, som jag visade i mitt förra inlägg
Vad är det man ska skriva att det gäller för då för de deriverade funktionerna?
Ture skrev:
Yes jag korrigerade. Det är alltså fel på sättet jag satte olikheten på .
Jag vet ej varför jag får att x=1/4 är en lokal min i min teckentabell. Vad är felet här?

Tillägg: 24 okt 2023 22:25
Edit jag kom på varför det är fel.