Ansättning

Jag tror det är så här

1+2+3+…+n blir ett andragradsuttryck   (1)

1²+2²+3²+…+n² blir ett tredjegradsuttryck   (2)

…

1^k+2^k+3^k+…+n^k blir ett uttryck av grad k+1.    (k)

Jag lovar inte att (k) är sant, men jag vet att (1) och (2) är sanna.

Så vi ansätter

1²+2²+…+n² = A+Bn+Cn²+Dn³

Sätt in n = 0, det ger A = 0.

Sätt in n = 1, det ger A+B+C+D = 1² (men A kan strykas eftersom det är noll)

Sätt in n= 2, det ger  2B+4C+8D = 1²+2²

Sätt in n = 3, det ger …

Du har nu tre ekvationer och tre obekanta. Bestäm B, C, D

Nu har du en formel. Om man inte litar hundra på att (2) gäller, så kan man troligen visa den med t ex ett induktionsbevis.

Kanske är det precis detta som står i boken du kopierat, den texten ser jag bara fragment av.

Jag kan glädja dig med att jag nog har bevisat (k) en gång, men jag har glömt hur jag isåfall gjorde.

Marilyn har rätt

Utgå från

(k+1)^3 - k^3 = 3k^2+3k+1

och summera från 1 till n på båda sidor.

VL blir en teleskopsumma som blir (n+1)^3-1 och HL innehåller sökt summa och summor av lägre grad som är enkla att bestämma.

Sedan håller man på så och arbetar sig upp i gradtalen till godtycklig grad. Lite tråkiga räkningar dock.

Tack Trinity2, det känner jag igen. Och räkningarna är enahanda som du säger.

Marilyn skrev:

Tack Trinity2, det känner jag igen. Och räkningarna är enahanda som du säger.

Och när graderna stiger... pust...

Den här tycker jag är trevlig

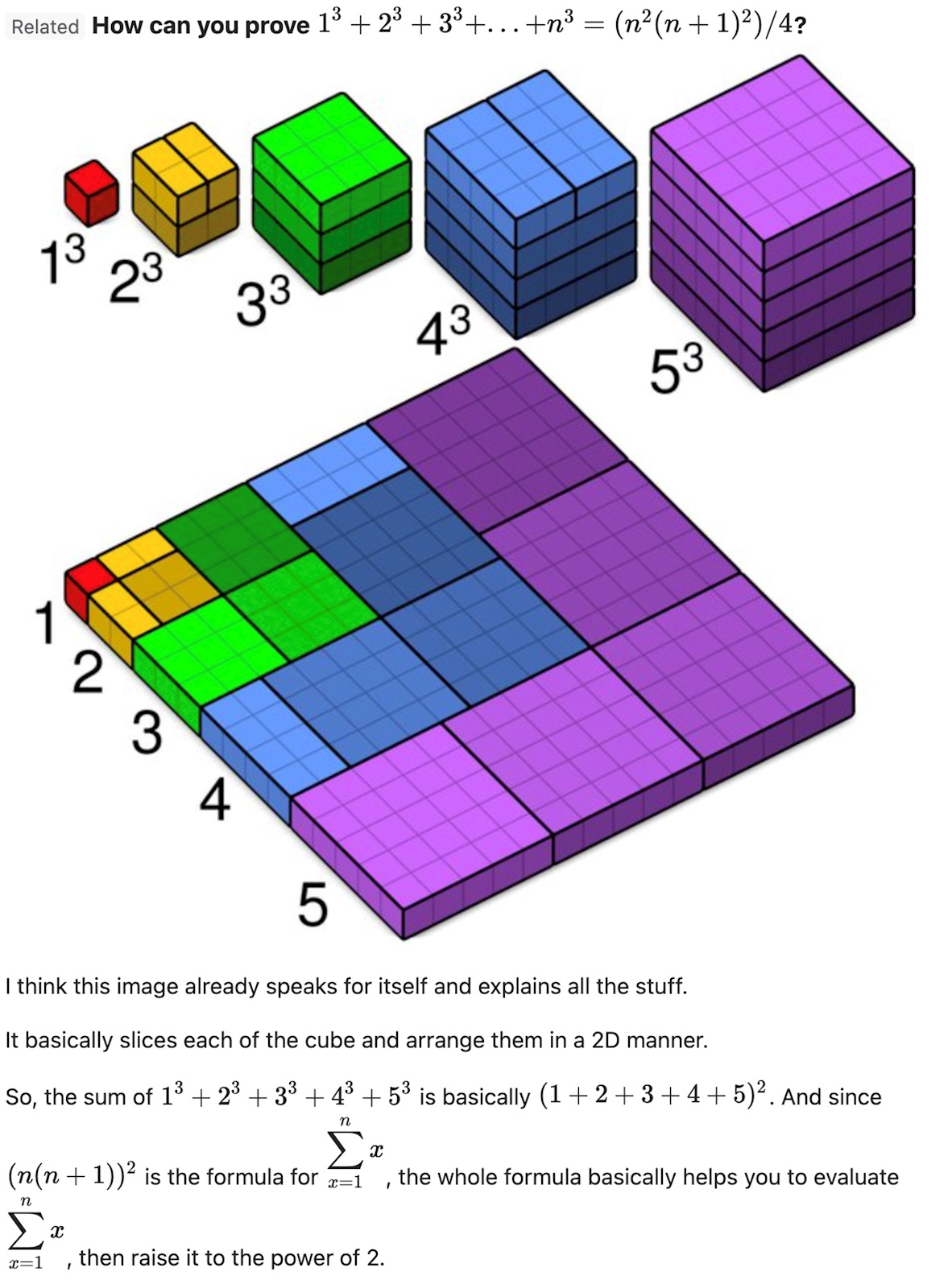
Den var snygg. Något att titta på när man ber sin aftonbön.

Marilyn skrev:

Den var snygg. Något att titta på när man ber sin aftonbön.

På altaret står bilder av Gauss, Euler och Newton... Du skall inga Gudar hava jämte mig…… Vi matematiker är polyteister

Hej! Bara en liten fråga, hur är detta matte för åk 9? Blev lite chockad för jag går själv i nian och har aldrig stött på sådana frågor, så nu när NP närmar sig blir man ju lite nojig 

Svårt att säga hur detta skulle komma in i nians kurs. Bilderna ur boken är så hårt beskurna att förutsättningarna för uppgiften inte framgår.

Ja, jag tänkte mer eftersom att tråden var publicerad under matte åk 9, men då var det inget att oroa sig för :)

Det KANSKE är en åk 9-uppgift, jag kan inte bedöma det. 

Marilyn skrev:

Svårt att säga hur detta skulle komma in i nians kurs. Bilderna ur boken är så hårt beskurna att förutsättningarna för uppgiften inte framgår.

de var beskurna för att jag endast ville ha med formlerna med variablerna :)

Det står i boken att det är mest till för gymnasieelever, men även högstadieelever! Jag går i nian, därför är de under åk9

Oki, tack! 

Marilyn skrev:

Jag tror det är så här

1+2+3+…+n blir ett andragradsuttryck   (1)

1²+2²+3²+…+n² blir ett tredjegradsuttryck   (2)

…

1^k+2^k+3^k+…+n^k blir ett uttryck av grad k+1.    (k)

Jag lovar inte att (k) är sant, men jag vet att (1) och (2) är sanna.

Så vi ansätter

1²+2²+…+n² = A+Bn+Cn²+Dn³

Sätt in n = 0, det ger A = 0.

Sätt in n = 1, det ger A+B+C+D = 1² (men A kan strykas eftersom det är noll)

Sätt in n= 2, det ger  2B+4C+8D = 1²+2²

Sätt in n = 3, det ger …

Du har nu tre ekvationer och tre obekanta. Bestäm B, C, D

 

Nu har du en formel. Om man inte litar hundra på att (2) gäller, så kan man troligen visa den med t ex ett induktionsbevis.

Kanske är det precis detta som står i boken du kopierat, den texten ser jag bara fragment av.

Jag kan glädja dig med att jag nog har bevisat (k) en gång, men jag har glömt hur jag isåfall gjorde.

Hur vet man vad man ska ansätta? Jag har läst att det ofta krävs en kvalificerad gissning, stämmer detta?

Hur man vet vad man ska ansätta?

Det bygger på en kvalificerad gissning, ja.

Ibland på kunskap, ibland på erfarenhet.

I detta fall, 1²+2²+3²+…+n² så är det nästan omöjligt för den niondeklassare som saknar kunskap och erfarenhet att gissa. Ska jag ansätta A*2ⁿ + B eller något annat???

Men i boken tycks det finnas en hint: Ansätt A+Bn+Cn²+Dn³. Jag vet inte om boken motiverar varför man just ska ansätta det polynomet, varför man inte behöver lägga till En⁴ och Fn⁵ osv. Eller varför Dn³ måste vara med. Själv tycker jag kanske att det skulle räcka att man provar den föreslagna ansättningen och bestämmer A, B, C, D. Redan det är en del arbete med rika möjligheter till slarvfel, I have been there.

När man har bestämt konstanterna, kan man prova att ”den verkar gälla” genom att sätta in n = 4 och n = 5.

Nästa steg är svårare. Hur vet vi att den funkar för n = 279653? Vi kan inte prova för alla alla n, vi måste hitta ett generellt bevis för alla positiva heltal n. En möjlighet är ett induktionsbevis, men det tror jag inte kommer förrän i gymnasiet. Jag tror många niondeklassare kan förstå ett bevis, men det ligger nog utanför kursinnehållet (länge sedan jag uppdaterade mig där).

Som sagt, jag har inte sett boken, jag kommer inte så mycket längre. Kanske är uppgiften tänkt som litet spännande bredvidläsning för elever som känner sug efter något utanför kursens upptrampade stig?

Som Marilyn skriver är det mycket erfarenhet och "högre kunskap" som gör att man "ser" detta.

Rent intuitivt kan du tänka dig att du staplar "något kvadratisk" = "något^2" = areor på varandra. Gör man detta får man "volym". Om du t.ex. lägger ut flera papperslappar på ett bord har du "areor", om du sedan staplar dem på varandra får du till slut en hög med papper, en "volym papper", och volymer mäter vi med "^3" (tre dimensioner). Det ger en *fingervisning* om vad det kan tänkas vara (och hur det växer med n) även om det inte är ett vattentätt matematiskt bevis. Ibland får man gissa i matematiken och har man tur gissade man rätt.

Trinity2 skrev:

Som Marilyn skriver är det mycket erfarenhet och "högre kunskap" som gör att man "ser" detta.

Rent intuitivt kan du tänka dig att du staplar "något kvadratisk" = "något^2" = areor på varandra. Gör man detta får man "volym". Om du t.ex. lägger ut flera papperslappar på ett bord har du "areor", om du sedan staplar dem på varandra får du till slut en hög med papper, en "volym papper", och volymer mäter vi med "^3" (tre dimensioner). Det ger en *fingervisning* om vad det kan tänkas vara (och hur det växer med n) även om det inte är ett vattentätt matematiskt bevis. Ibland får man gissa i matematiken och har man tur gissade man rätt.

Bra förklaring!

Summan 1+2+3+…+n kan ses som att man lägger ut n linjaler intill varandra. Den första har längd 1, den andra har längd 2, den tredje längd 3 osv.

Det blir som en rätvinklig triangel med vardera katetern längd n. Summan är lika med triangelns area som är n * n / 2. Fast nu är hypotenusan litet taggig, så vi får modifiera:

n * (n–1) / 2.

Hur man ska modifiera kan man avgöra med insättning. Och, som Trinity2 skriver, kan man bygga en pyramid av kvadratskivor – en volym.

Areor: andragradsuttryck — Volymer: tredjegradsuttryck.

När man sedan fortsätter med 1³ + 2³ + … + n³ , 1⁴ + 2⁴ + … + n⁴ osv, så visar sig universums ofullständighet. Vi har inte tillräckligt med dimensioner för att åskådliggöra dessa summor. Men matematiken är inte så inskränkt som vårt trånga universum; vi kan obekymrat bygga vidare med polynom av godtycklig grad.